设随机变量X服从参数为(2,p)的二项分布,随机变量Y服从参数为(3,p)的二项分布,若P{X≧1

P（X＞1）＝5／9

而P（X＞1）＝P（X＝2）＝P＾2＝5／9

P＝1／3＊√5

P（Y＞1）＝P（Y＝2）＋P（Y＝3）＝3P＾2＊（1－P）＋P＾3

＝3P＾2－2P＾3

＝3＊5／9－2（1／3＊√5）＾3

＝5／3－10／27＊√5

P(X>1)=P(X=2)=p^2=5/9.

得p=根号5 /3。P(y>1)=P(Y=2)+P(Y=3)

＝3＊（p＾2）＊（1－p）＋p＾3

＝（5／9）＊（3－2＊（根号5）／3）。

扩展资料

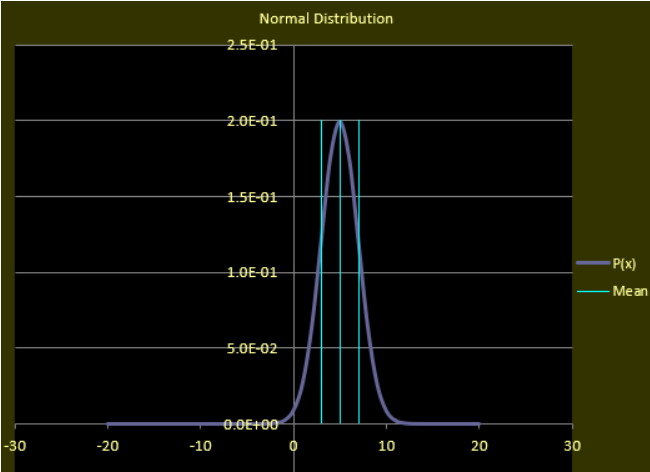
正态分布密度函数的特点：

均值μ为对称轴。

标准差σ表示图形的宽窄，标准差越小，数值越向平均值靠拢（可以理解为标准差是到均值的平均距离）

二项分布是有限的，正态分布在整个实轴上都有定义，即概率密度不会等于0。（尽管延伸出去概率极小，但也是存在的）