【Mathematica】基于极坐标变换的图像变形

1、给一张正方形图片。

2、Mathematica进行图像变换的时候，总是把正方形图片放到平面上的0和1之间的小正方形内部。相当于右上角像素的坐标是{1,1}。注意看代码中的PlotRange的范围。

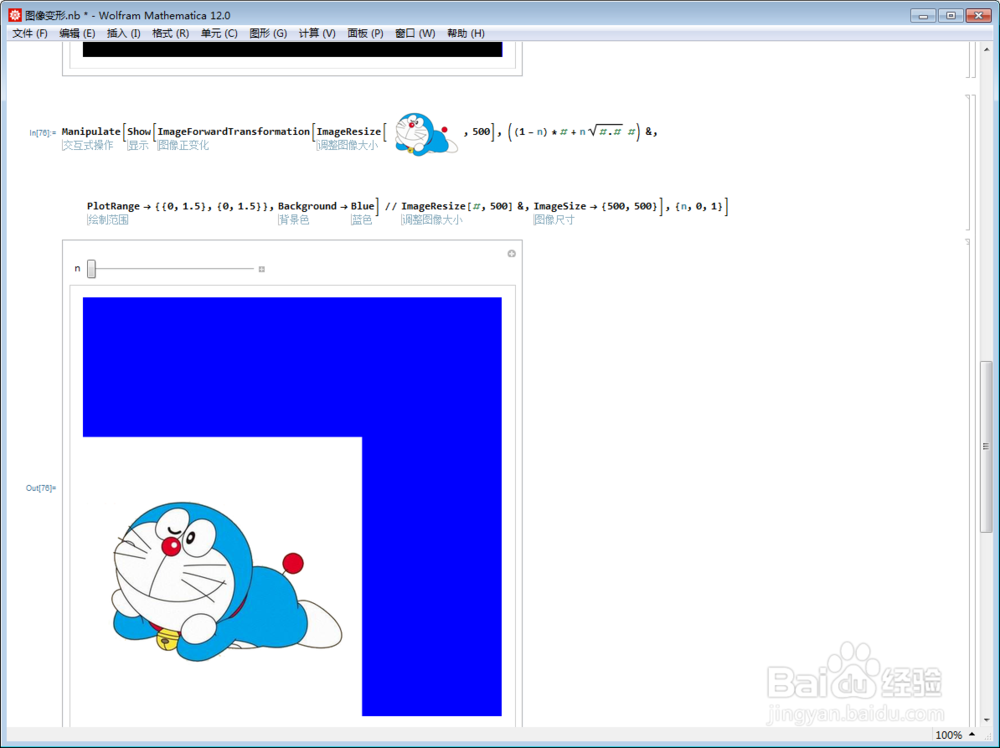
3、上面的变换，当n=1的时候，相当于把极坐标点{ρ，θ}变为{ρ^2，θ}。设这个点的直角坐标是{x,y}，那么ρ=Sqrt[{x,y}.{x,y}]，那么变换之后的点的直角坐标就是：{ρ*x，ρ*y}这个点到原点的距离是ρ^2。

4、关于变量n的动画是：

5、如果要把正方形图片的中心置于原点，就需要把坐标减去0.5。

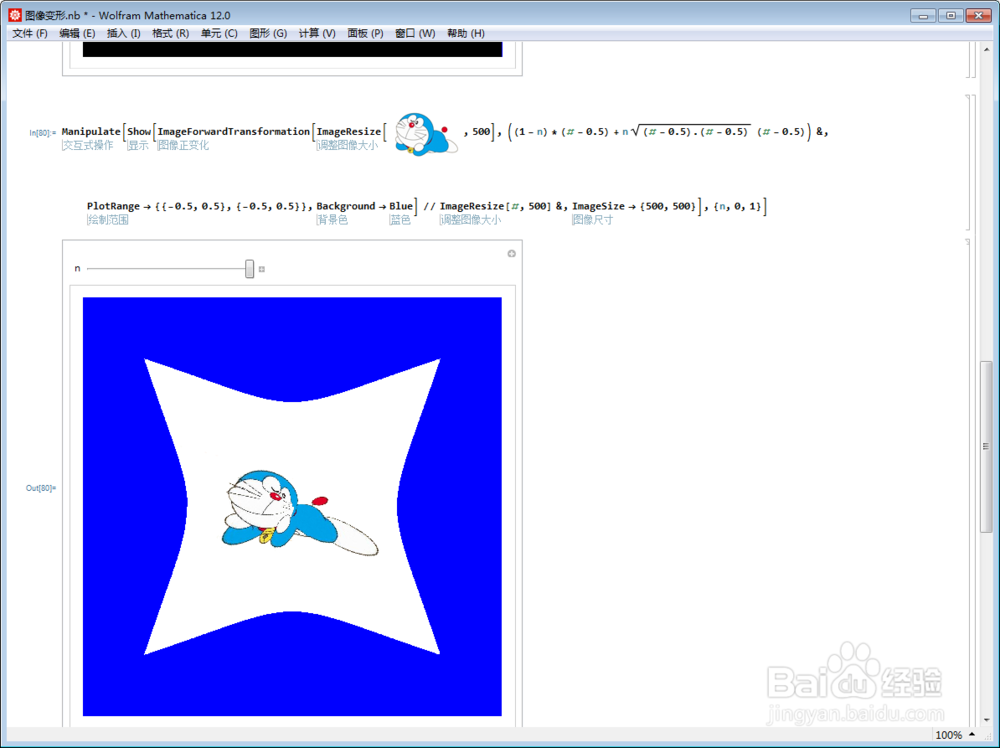
6、此时进行极坐标变换：ρ→ρ^2，得到如下效果。

7、动态图如下：

8、如果极坐标变换改为：ρ→Sqrt[ρ]，代码如下（以图片中心为原点）：

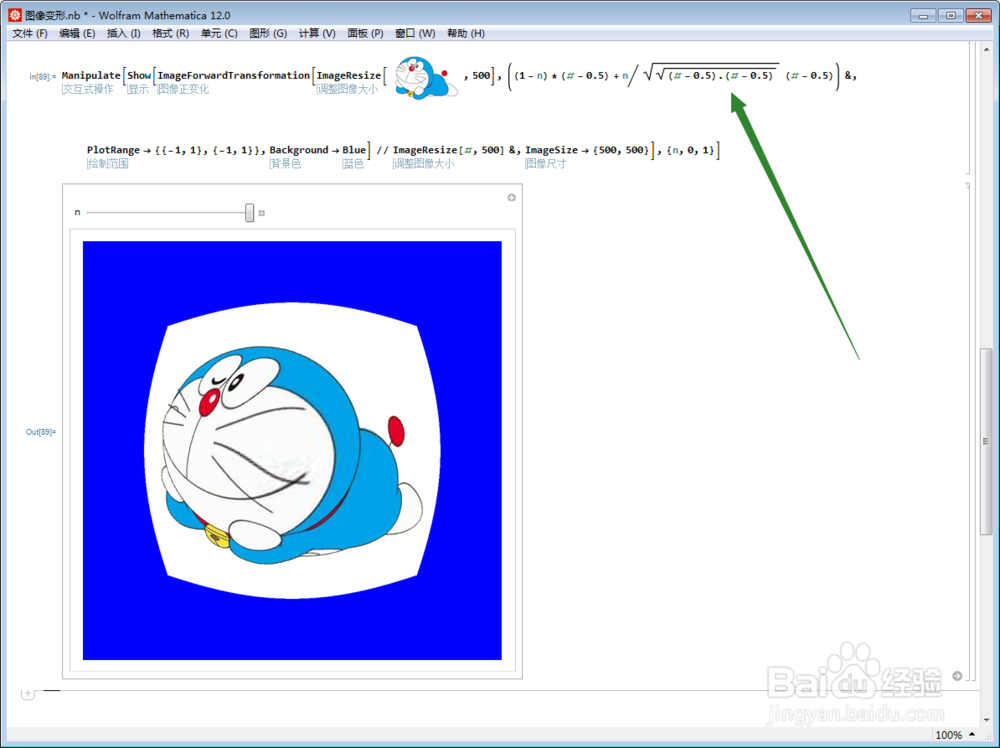
9、对应的动态图是：

10、如果极坐标变换改为：ρ→Sqrt[ρ]，且以图片左下角为原点，动态图如下：