【抽象代数】正八面体对称群的表示

1、除了恒等变换，绕着x轴的旋转对称还包括90°、180°、270°的旋转，其中，把绕着x轴的90°旋转记为a，那么，a的矩阵形式可以写为：

a = RotationMatrix[Pi/2, {1, 0, 0}]

绕着x轴的180°、270°的旋转，可以记为a.a、a.a.a。

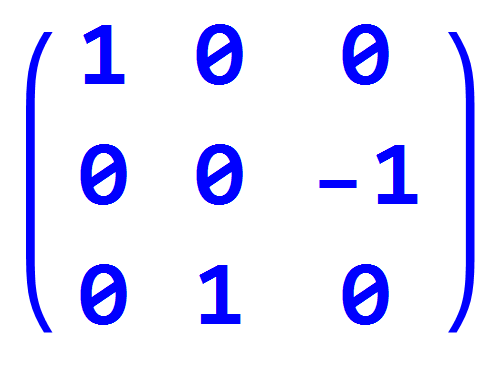
2、绕着y轴旋转90°的矩阵形式记为b：

b = RotationMatrix[Pi/2, {0, 1, 0}]

对应的还有b.b、b.b.b。

3、绕着z轴旋转90°的矩阵形式，记为c：

c = RotationMatrix[Pi/2, {0, 0, 1}]

还有对应的c.c、c.c.c。

4、上面这些变换，实际上是绕着某个顶点与正八面体的中心的连线的旋转。

然后，再列举绕着某个面的中心与正八面体的中心的连线的旋转。

绕着向量 {1, 1, 1} 的120°旋转记为d，那么，d.d就表示绕着向量 {1, 1, 1} 的240°旋转：

d = RotationMatrix[2*Pi/3, {1, 1, 1}];

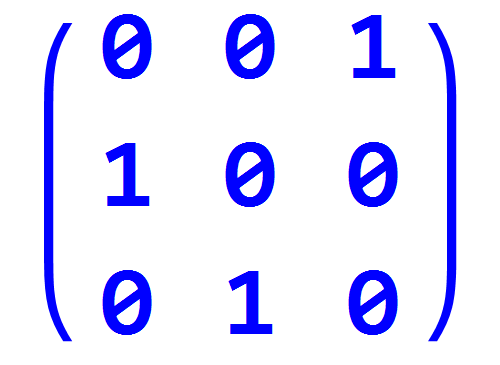
5、还有绕着向量{1, -1, 1}、{-1, 1, 1}、{-1, -1, 1}的120°旋转，其矩阵形式分别记为e、f、g：

e = RotationMatrix[2*Pi/3, {1, -1, 1}];

f = RotationMatrix[2*Pi/3, {-1, 1, 1}];

g = RotationMatrix[2*Pi/3, {-1, -1, 1}];

还有对应的e.e、f.f、g.g。

下图是矩阵e。

6、绕着某条棱的中点与正八面体的中心的连线的旋转，都是180°的旋转。

正八面体有12条棱，对应棱的旋转可以视为同一个变换，这样，12条棱可以分为6对，就有六个180°的变换，分别记为：h、i、j、k、l、m：

h = RotationMatrix[Pi, {1, 0, 1}];

i = RotationMatrix[Pi, {0, 1, 1}];

j = RotationMatrix[Pi, {-1, 0, 1}];

k = RotationMatrix[Pi, {0, -1, 1}];

l = RotationMatrix[Pi, {1, 1, 0}];

m = RotationMatrix[Pi, {1, -1, 0}];

下图是h的矩阵形式。

7、再算上恒等变换（矩阵形式是单位矩阵），可以发现，正八面体群共有24个元素。它们的旋转矩阵表示，在下表中列出。