MATLAB计算等额本金和等额本息(哪种方式更合适)
1、首先介绍等额本金,等额本息的概念、特点和计算公式。
等额本金是指还款期内,把贷款总额等分,每月还相同数额的本金和剩余贷款在该月产生的利息。特点是每月还款金额递减(每月还款本金固定,利息越来越少),借款人起初还款金额较大,越往后每月还款金额越少。
等额本息是指还款期内,把本金总额与利息总额相加,然后平均分摊到还款期内的每个月中。特点是每个月的还款金额固定,每月还款中的本金比重逐月递增,利息比重逐月递减。
下图是等额本金和等额本息的计算公式。
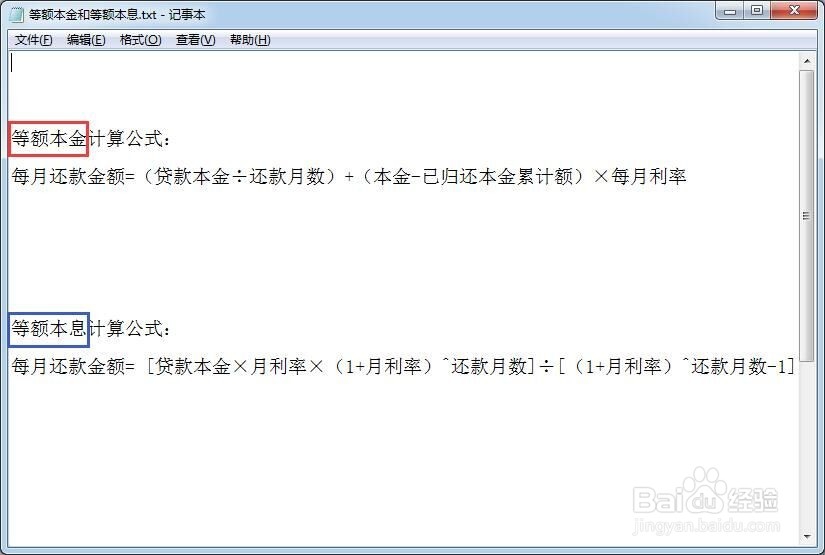
2、举例计算:假如有88万住房贷款,其中70万公积金贷款(年利率3.25%),18万商业贷款(年利率4.9%),贷款期限20年。
那么分别采用等额本金、等额本息两种方式,每月还款金额和累积还款金额是多多少?
是选择等额本金还是选择等额本息?

3、下面使用MATLAB计算上边的例题:
(1)计算等额本金、等额本息两种方式的每月还款金额。
(2)计算等额本金、等额本息两种方式的20年(240月)累积还款金额。
(3)画出等额本金、等额本息两种方式,每月还款金额、累积还款金额随时间的变化图。
(4)计算等额本金每月递减多少?
(5)计算第几月或第几年,等额本金开始小于等额本息的月还款金额。
(6)计算第几月或第几年,等额本金开始小于等额本息的累积还款金额。
代码如下:
clear all;close all;clc;dbstop if error
gdai=700000; % 公积金贷款70万
gxi=0.0325; % 公积金贷款年利率3.25%
sdai=180000; % 商业贷款18万
sxi=0.049; % 商业贷款年利率4.9%
m=12*20; % 贷款期限20年(240月)
x=1:m;
% “等额本金”的每月还款金额(yg1=)
gdai1=gdai/m;
sdai1=sdai/m;
for i=1:m
yg1a(i)=gdai1+(gdai-gdai1*(i-1))*(gxi/12);
yg1b(i)=sdai1+(sdai-sdai1*(i-1))*(sxi/12);
yg1(i)=yg1a(i)+yg1b(i);
end
% “等额本息”的每月还款金额(yg2=)
gxii=gxi/12;
sxii=sxi/12;
for i=1:m
yg2a(i)=(gdai*gxii*(1+gxii)^m)/((1+gxii)^m-1);
yg2b(i)=(sdai*sxii*(1+sxii)^m)/((1+sxii)^m-1);
yg2(i)=yg2a(i)+yg2b(i);
end
% “等额本金”和“等额本息”的累积还款
sumyg1(1)=yg1(1);
sumyg2(1)=yg2(1);
for i=2:m
sumyg1(i)=sumyg1(i-1)+yg1(i);
sumyg2(i)=sumyg2(i-1)+yg2(i);
end
disp('在命令窗口输出“等额本金”每月还款(yg1=)、每月累积还款(sumyg1=)')
yg1
sumyg1
fprintf('在命令窗口输出“等额本息”每月还款(yg2=)、\r每月累积还款(sumyg2=)\n')
yg2
sumyg2
subplot(2,1,1); plot(x,yg1, 'r', x,yg2, 'b', 'LineWidth',2)
axis([0,m,2500,6500])
set(gca,'xtick',[0:24:m],'ytick',[2500:500:6500])
set(gca,'FontName','Time New Roman','FontSize',10,'FontWeight','bold')
xlabel('')
ylabel('每月还款(元)')
text(x(106),yg1(106),'x')
text(x(106),yg1(106)+195,'8.8年')
legend('等额本金','等额本息')
title('\fontsize{15}住房房贷:等额本金VS等额本息',...
'FontWeight','bold','FontAngle','italic','Color','r')
subplot(2,1,2); plot(x,sumyg1,'r', x,sumyg2,'b', 'LineWidth',2)
xlim([0,m]);ylim([1000,1.5e+06])
set(gca,'xtick',[0:24:m],'ytick',[50000:200000:1500000])
set(gca,'FontName','Time New Roman','FontSize',10,'FontWeight','bold')
xlabel('时间序列(20年, 240月)')
ylabel('累积还款(元)')
text(x(212),sumyg1(212)+20000,'x')
text(x(212)-5,sumyg1(212)-100000,'17.6年')
text(x(240)-7,sumyg1(240)-50000,'119.7万元')
text(x(240)-7,sumyg2(240)+50000,'123.6万元')
disp('“等额本金”每月递减多少(diff=),format long小数点后15位,short小数点后4位')
format long
diff=yg1(1)-yg1(2)
format short
diff=yg1(100)-yg1(101)
disp('第几月或第几年,等额本金开始小于等额本息的月还款金额')
for i=1:m
if yg1(i)<=yg2(i)
fprintf('第i月,i=%i\n',i)
fprintf('第i年,i=%4.1f\n',i/12)
break
end
end
fprintf('\r第几月或第几年,等额本金开始小于等额本息的累积还款金额\n')
for i=1:m
if sumyg1(i)<=sumyg2(i)
fprintf('第i月,i=%i\n',i)
fprintf('第i年,i=%4.1f\n',i/12)
break
end
end
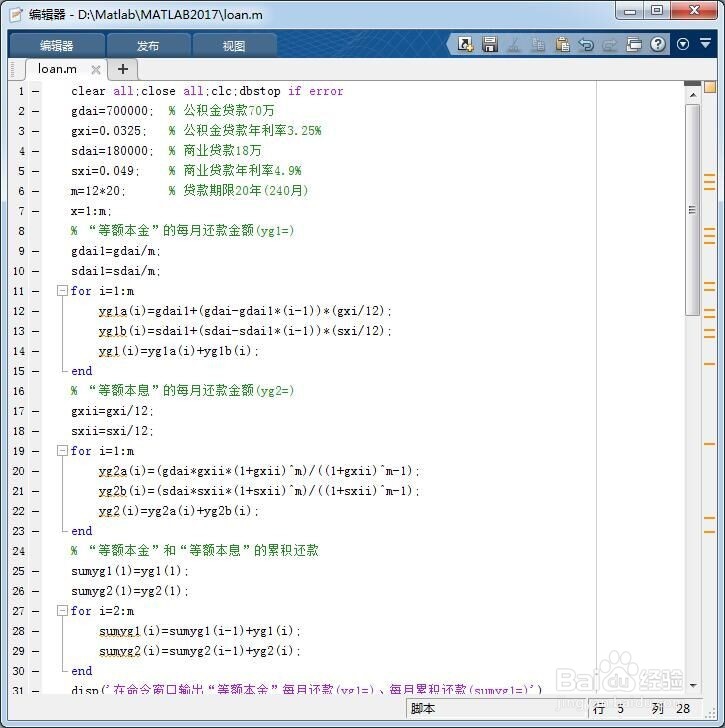
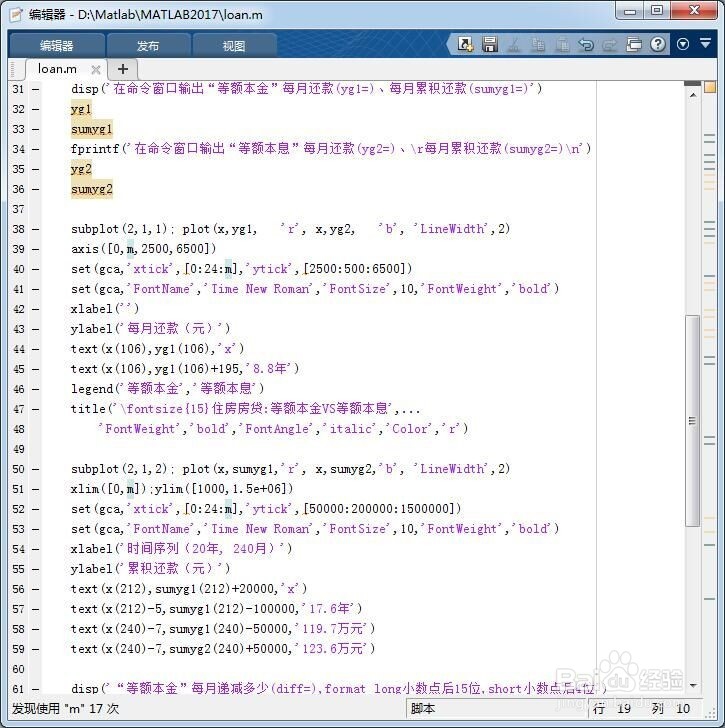
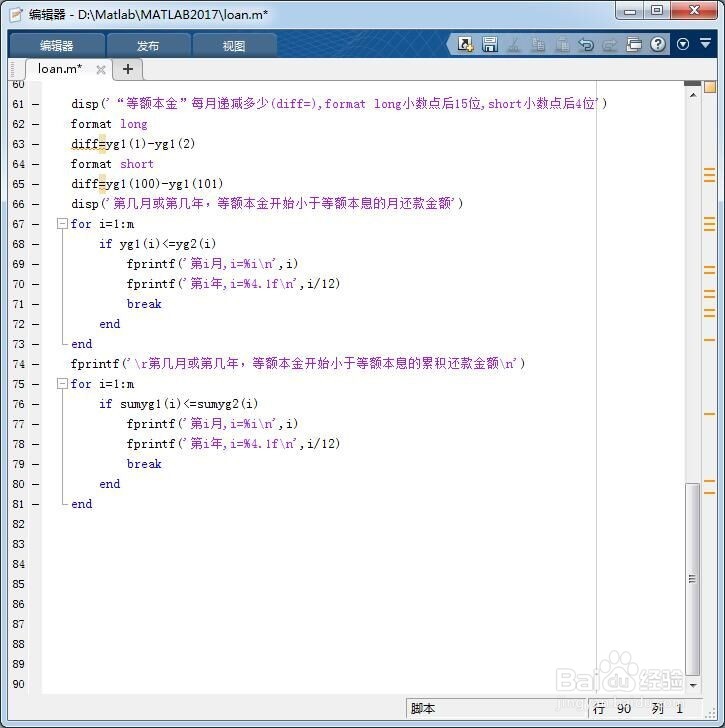
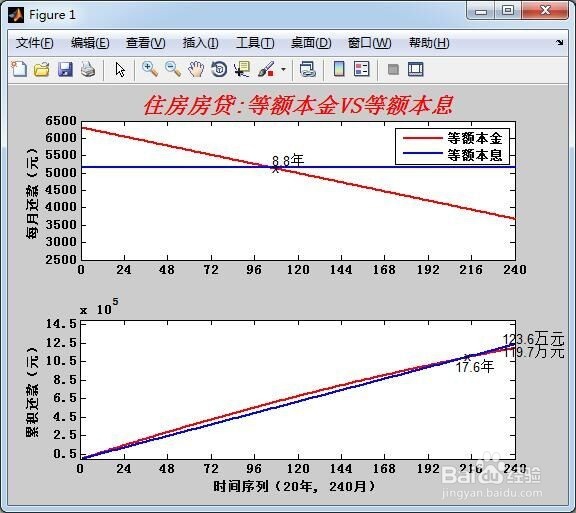
4、在MATLAB编辑器中点击保存和运行上述代码,得到如下图像。
可以发现:
(1)从每月还款金额看:等额本金递减(开始每月还款6297.5元,最后每月还款3677.6元,逐月递减10.96元);等额本息不变(每月还款5148.4元)。从第106个月(8.8年)起,等额本金的每月还款金额开始小于等额本息。
(3)从累积还款金额看:等额本金累积还款119.7万元,等额本息累积还款123.6万元,两者相差近4万元(抛开20年货币贬值与否)。从第212个月(17.6年)起,等额本金的累积还款金额开始小于等额本息。
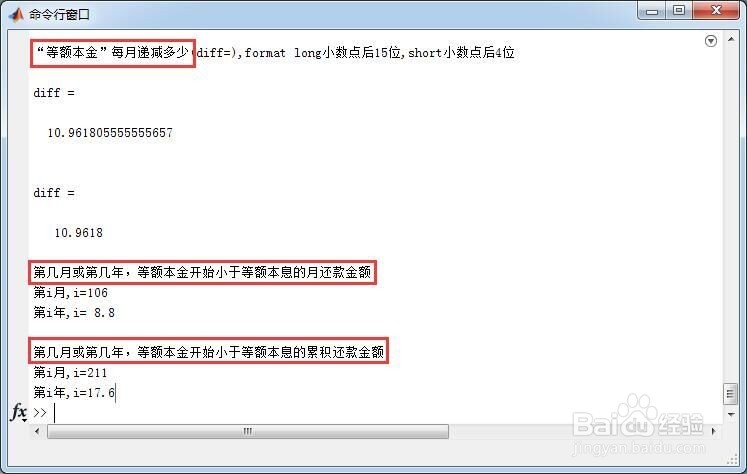
5、在命令窗口,可以找到以下三个问题的答案。
(1)“等额本金”每月递减多少?
(2)第几月或第几年,等额本金开始小于等额本息的月还款金额?
(3)第几月或第几年,等额本金开始小于等额本息的累积还款金额?
6、总结而言,在贷款金额、利率和期限相同的情况下,等额本金和等额本息相比:
(1)还款初期,等额本金每月还款金额大于等额本息,但在还款后期,等额本金每月还款金额小于等额本息。
(2)最终结算,等额本金相对于等额本息所还款总额要少,利息也少,但等额本金刚开始时还款压力较大。
(3)等额本金适合有一定经济基础,能够承担前期较大还款压力、且有提前还清计划的借款人。
(4)等额本息因每月还款相同,方便安排收支,适合经济条件不允许前期还款过大的借款人。
If you are intereting in this, please fellow me and give some comments, Thanks.
