定积分值为零有哪些特殊情况(尽量列全一点)
三种情况:①被积函数为y = 0,即直线的面积为0(线段有长没有宽,直线是无限长的,也没有宽,所有都没有面积),可推断出定积分值为零。
②积分的上限和下限相同,并且上下限只是一个形式而已,位置不一样而已,在积分的外面加一个负号,则积分的上限和下限互换,
③在对称区间(- a,a)上,被积函数为奇函数,定积分所形成的图像正负面积抵消,故有定积分结果等于0。
扩展资料:
一般定理
定理1:设f(x)在区间[a,b]上连续,则f(x)在[a,b]上可积。
定理2:设f(x)区间[a,b]上有界,且只有有限个间断点,则f(x)在[a,b]上可积。
定理3:设f(x)在区间[a,b]上单调,则f(x)在[a,b]上可积。
牛顿-莱布尼茨公式:
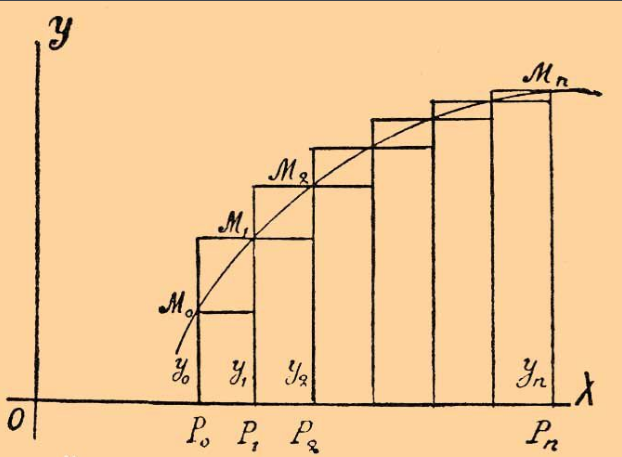
定积分与不定积分看起来风马牛不相及,但是由于一个数学上重要的理论的支撑,使得它们有了本质的密切关系。把一个图形无限细分再累加,这似乎是不可能的事情,但是由于这个理论,可以转化为计算积分。这个重要理论就是大名鼎鼎的牛顿-莱布尼兹公式,它的内容是:
如果f(x)是[a,b]上的连续函数,并且有F′(x)=f(x),那么
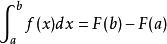
正因为这个理论,揭示了积分与黎曼积分本质的联系,可见其在微积分学以至更高等的数学上的重要地位,因此,牛顿-莱布尼兹公式也被称作微积分基本定理。
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:91
阅读量:107
阅读量:179
阅读量:167
阅读量:125