使用Scikit-Learn和Pandas学习线性回归模型优化
1、首先我么需要下载公开的数据(循环发电厂的数据)供我们跑机器学习的线性模型,该数据的属性主要有以下5个列属性:
1)AT(温度),
2) V(压力),
3) AP(湿度),
4) RH(压强),
5)PE(输出电力)。



2、其次,明确我们的研究目的,就是使用这些数据得到一个线性的关系,对应PE是样本输出,利用AT/V/AP/RH这4个是样本特征属性, 得到一个线性回归模型,即:PE=θ_0+θ_1*AT+θ_2*V+θ_3*AP+θ_4*RH,我们需要通过数据学习的θ_0、θ_1、θ_2、θ_3、θ_4这5个参数。
3、现在我们需要对下载的数据进行整理
1)对数据文件进行解压缩
2)将xls文件另存为csv文件供我们进行下一步的处理

4、导入相关的Python依赖库,读取数据文件
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn import datasets, linear_model
# read_csv里面的参数是csv在你电脑上的路径
data = pd.read_csv('F:\ML\CCPP\CCPP\Folds5x2_pp.csv')
#测试打印前5行数据
print(data.head())

5、识别数据的维度信息,通过 data.shape可以识别出数据为(9568, 5):
说明数据有9568个样本,每个样本数据有5列。

6、构建数据的样本特征
我们用AT, V,AP和RH这4个列作为样本特征属性,PE作为特征输出:
#样本特征
x = data[['AT', 'V', 'AP', 'RH']]
print(x.head())
#样本输出
y = data[['PE']]
print(y.head())

7、划分数据模型的训练集和测试集
我们把x和y的数据样本分为两部分数据集,A部分模型训练集,B部分是模型测试集,如下:
from sklearn.cross_validation import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=1)
print(x_train.shape)
print(y_train.shape)
print(x_test.shape)
print(y_test.shape)
输出结果为:
(7176, 4)
(7176, 1)
(2392, 4)
(2392, 1)
可以看到大概75%的数据到训练集,25%的数据到测试集

8、用scikit-learn的线性模型来拟合我们需要求解的问题,scikit-learn的线性回归算法使用的是最小二乘法来实现的。
#运行线性回归模型进行训练集数据的拟合训练
from sklearn.linear_model import LinearRegression
linearReg = LinearRegression()
linearReg.fit(x_train, y_train)
#拟合后可以得到模型系数结果:
print(linearReg.intercept_)
print(linearReg.coef_)
最后输出的结果如下:
intercept_:[460.05727267]
coef_:[[-1.96865472 -0.2392946 0.0568509 -0.15861467]]
这样我们就得到了在步骤2里面的需要求得的5个系数值:
PE=θ_0+θ_1*AT+θ_2*V+θ_3*AP+θ_4*RH
也就是说PE和其他4个变量的关系如下:
PE=460.05727267-1.96865472∗AT-0.2392946∗V+0.0568509∗AP-0.15861467∗RH

9、有了我们的训练集输出模型,我么需要评估我们的模型的好坏程度,对于线性回归来说,我们用均方差(Mean Squared Error, MSE)或者均方根差(Root Mean Squared Error, RMSE)在测试集上的表现来评价模型的好坏。
我么需要根据测试集的x特征数据预预测的y数据,最后根据测试集y特征值与预测的特征值进行比对,输出我们模型的MSE和RMSE,MSE说明了我们的模型预测值和测试集y的差异。
------------------
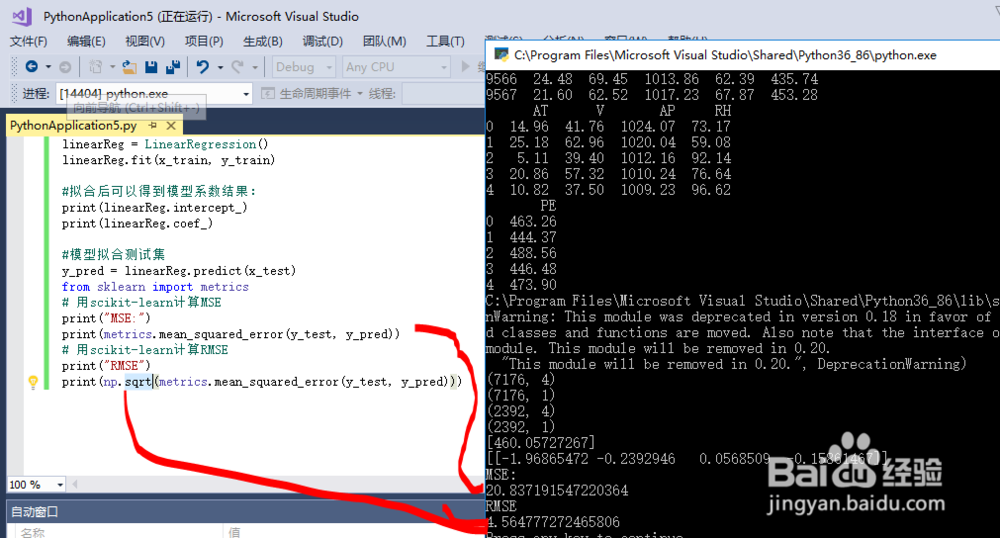
#模型拟合测试集
y_pred = linearReg.predict(x_test)
from sklearn import metrics
# 用scikit-learn计算MSE
print("MSE:")
print(metrics.mean_squared_error(y_test, y_pred))
# 用scikit-learn计算RMSE
print("RMSE")
print(np.sqrt(metrics.mean_squared_error(y_test, y_pred)))
10、如何优化我们的模型
我们可以使用AT, V,AP和RH中的2个或3个进行交叉验证,看看使用2个或3个特征属性值得到的拟合模型,最后的MSE的值差别 ,MSE值越小说明该模型越准确,这样我们就可以进行模型的优化,获得到最好的模型。
11、最后我们通过画图的方式显示真实值和预测值的变化关系,离中间的直线y=x直接越近的点代表预测损失越低。
将测量值和预测值进行图表展现:
y_pred = linearReg.predict(x)
plt.figure()
plt.title("Model Star")
plt.xlabel("Measured")
plt.ylabel("Predicted")
plt.grid(True)
plt.plot(y,y_pred,'r.')
plt.show()
