Mathematica应用——有趣的绝对值方程
1、有一个有趣的问题:Abs[x y]+Abs[x-y+1]==0的图像是什么?
我冒冒失失的用Mathematica作图:
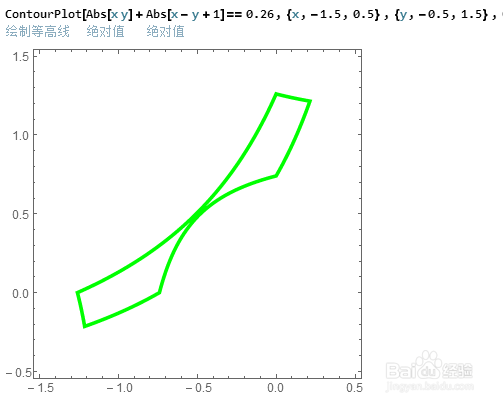
ContourPlot[Abs[x y]+Abs[x-y+1]==1,{x,-1.5,0.5},{y,-0.5,1.5}]
结果一无所获,即使扩大作图范围也不行。思考了一下之后,决定作对应的等高线图,并适当增加等高线的密度:
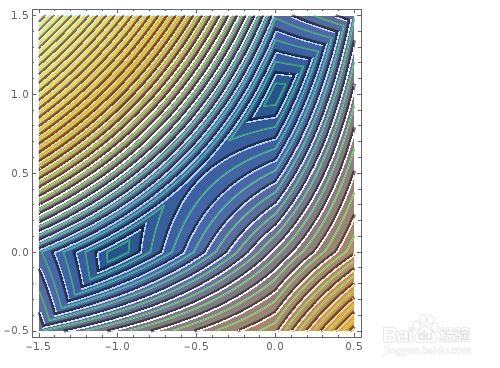
ContourPlot[Abs[x y]+Abs[x-y+1],{x,-1.5,0.5},{y,-0.5,1.5},Contours->60]
可以发现,当Abs[x y]+Abs[x-y+1]的值慢慢变小的时候,图像渐渐由一个整体裂开为两个部分,最后缩为两个点。
2、我比较感兴趣的是,如果Abs[x y]+Abs[x-y+1]==n的图像是一条曲线(而不是两条),那么n的最小值是多少?
初步估计,n不会小于0.25!
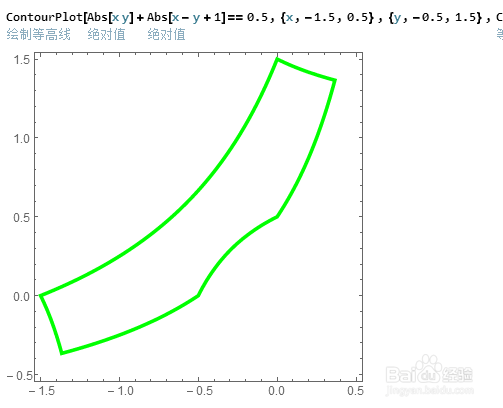
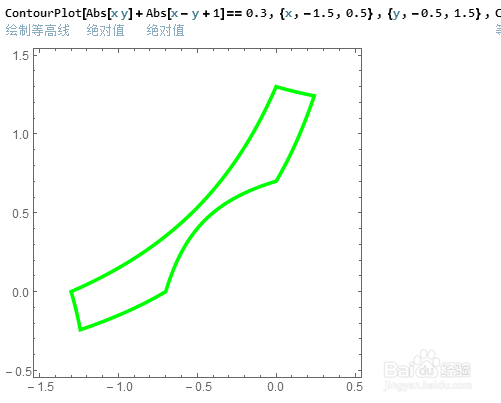

3、可以证明Abs[x y]+Abs[x-y+1]==n的图像是轴对称图形,对称轴是直线x+y=0。
观察发现,Abs[x y]+Abs[x-y+1]==n的图像是从对称轴附近先裂开的。所以当x+y=0和Abs[x y]+Abs[x-y+1]==n只有一个交点的时候,是图像从一支变成两支的临界点。
此时,x=-y,x^2+Abs[2x+1]==n有且仅有一个解。
于是,如果Abs[x y]+Abs[x-y+1]==n的图像是一条曲线(而不是两条),那么n的最小值是可求的!大家思考一下吧!

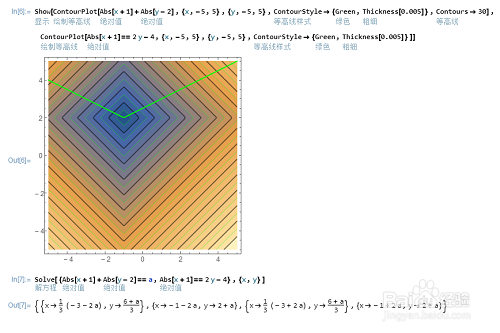
1、解方程组:{Abs[x+1]+Abs[y-2]==3,Abs[x+1]==2 y-4}
先分别画出这两个方程式对应的图像:
ContourPlot[{Abs[x+1]+Abs[y-2]==3,Abs[x+1]==2 y-4},{x,-5,5},{y,-5,5}]
Mathematica可以分别给这两个图像着不同的颜色。
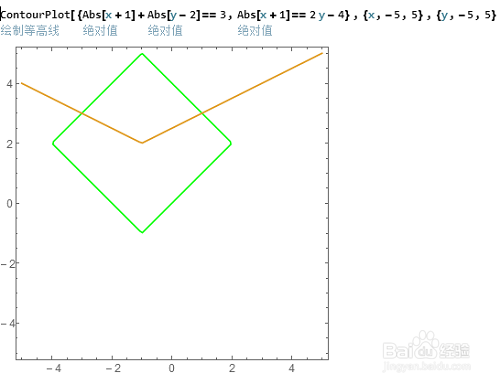
2、直接解这个方程组,是Mathematica的基本功能:
Solve[{Abs[x+1]+Abs[y-2]==3,Abs[x+1]==2 y-4},{x,y}]
有两个解,与图像相符!

3、可是,为什么在一般情况下,会有四个解呢?如下:
Assuming[a>0,Solve[{Abs[x+1]+Abs[y-2]==a,Abs[x+1]==2 y-4},{x,y}]]
具体的作图过程显示,不可能会有四个解啊!这是怎么回事?
原来是有增根,可以检测一下:
解=Solve[{Abs[x+1]+Abs[y-2]==a,Abs[x+1]==2 y-4},{x,y}]/.a->6
{Abs[x+1]+Abs[y-2]-6,Abs[x+1]-2 y+4}/.解