spss教程：对应分析

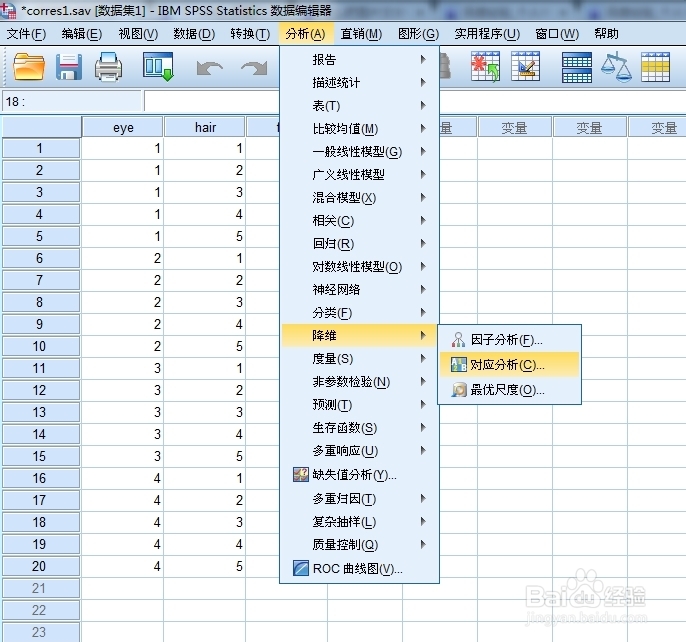
1、选着相关的变量分别作为列联表的行列变量，都是分类变量。

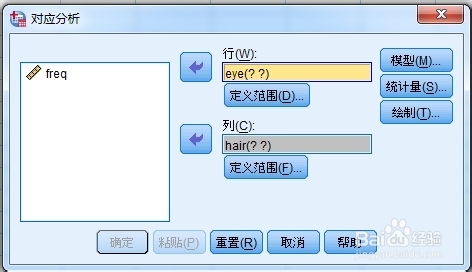
2、需定义各变量所取水平范围，“定义范围”按钮，键入最小值、最大值，然后点击按钮“更新”即可。

“类型约束”中常用“无”，定义分类特殊要求中，系统默认对分类没有特殊要求。行列变量的处理方法是一样的。

3、模型：

“解的维数”：在几维空间中求解，通常采用对应分析是将高维数据做低维处理，尽可能以小的维度解释多的变异，系统默认是2，至少在原先基础上维度降1个。

“距离度量”：卡方距离和欧式距离，这里选择卡方距离，列联表的卡方距离，即卡方统计量。

“标准化方法”：这里选择“行和列均值已删除”。

“正态化方法”：不同的正则化方法，对应分析产生不同的结果。系统默认的是对称正则化，行是列的加权均数，可分析变量间的差异性和相似性。

4、统计量：

对应表：输出原始对应表，即原始二维列联表。

行点概览：输出行变量的因子载荷和贡献。

列点概览：输出列变量的因子载荷和贡献。

行轮廓表：基于行合计的各格子的百分比。

列轮廓表：基于列合计的各格子的百分比。

对应表的排序：输出最优对应表。最大因子数，系统默认1。

置信统计量：

行点：行变量各点在各因子上的标准离差及相关系数。

列点：列变量各点在各因子上的标准离差及相关系数。

5、绘制：

“散点图”：“双标图”即在因子坐标中，行变量和列变量的散点对应图，反映行变量和列变量在因子上的对应关系，若以主成分进行正则化，不能输出该因子负荷图。这里就选择“双标图”。

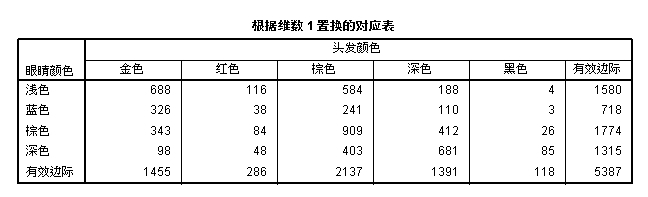
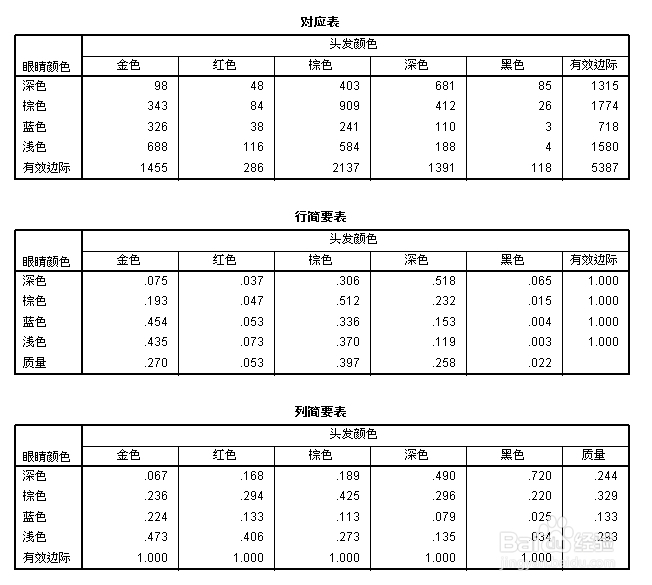
1、其中第一个即原始对应表，就是原始的二维频数分布表。接下来的是“行简要表”、“列简要表”，例如行简要表中，由对应表知，0.075=98/1315。

“质量”：0.270=1455/5387，其中的1455和5387分别是原始数据的统计量，质量是基于边际频数的影响量，为行或列百分比的加权均数，值越大，对形心影响越大，即越靠近形心。

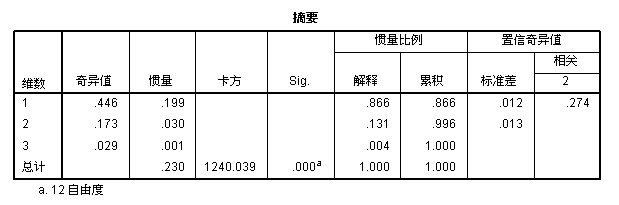
2、摘要：

降维数至3维（因子），是因为行列2变量中分类数最小的行变量的类数4减一个的结果。

奇异值：最好应该翻译成特征值，解释行与列因子分的相关性。

惯性值：等于各因子特征值的平方，例如0.3=0.173 x 0.173。

卡方：原始列联表的卡方检验。

“惯性比例解释”、“惯性比例累积”，解释因子的贡献率。

“置信奇异值”应该翻译成“置信特征值”，因为选择的是2维解，所以只给出两个因子的结果，标准差越小，说明点估计值越准确，因子的相关系数越小，则说明因子分解越稳定。

3、“概述行点”、“概述列点”，其中的“质量”还是上面图片中的结果，给出“维中的得分”、“贡献”，结果见图片。

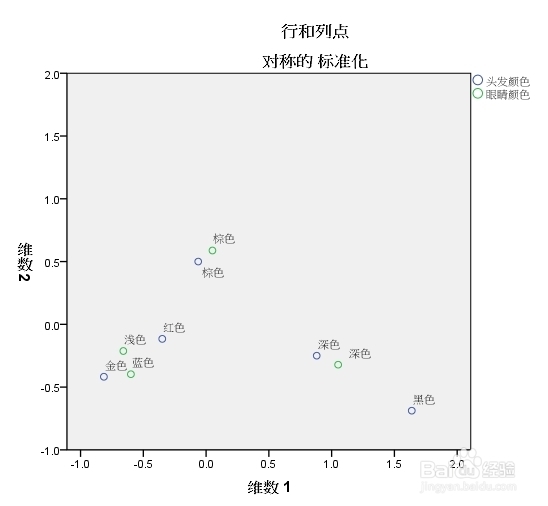
4、因子负荷图，可以看出哪些变量属于第一因子，哪些偏向于第二因子，图形很是直观。

基于第一因子的最优对应表，同因子负荷图一样，可以反映行列变量间的相关性。与原始的对应表可知，行列变量的顺序有所变动，观察可知，颜色深对应颜色深的，浅的对应浅的。