用Mathematica演示圆的各种摆线——外摆线

我在《用Mathematica演示圆的各种摆线——内摆线》里面介绍了用Mathematica模拟内摆线的过程，并把摆线归类为内摆线的一种。同样地，眺螗熨膣本文介绍用Mathematica模拟外摆线的过程，并把渐开线归类为外摆线的一种。 为了防止“土地公”剽窃，特意在动态图前面加了各种封面。这样，如果他们盗取的动态图变成静态图，那么就没有什么意义了！把代码放到动态图后面，那么获取代码的方法是把动态图导入到Mathematica里，查看后面几帧。 具体的方法，请参考：《用Mathematica修改图片大小》和《怎么用Mathematica修改gif图片的尺寸》。再用Mathematica提取图片中的文字。

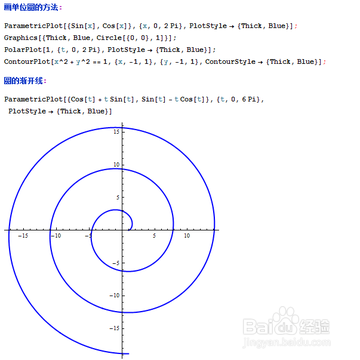
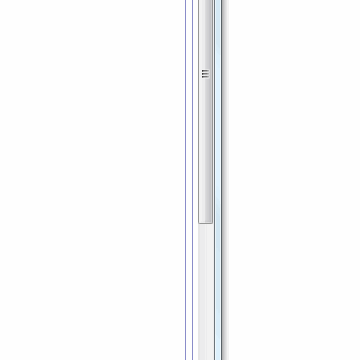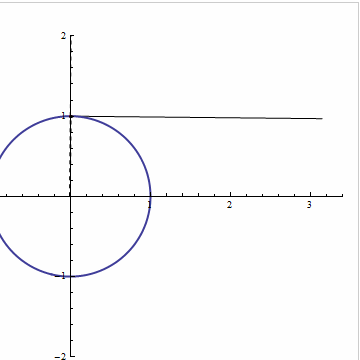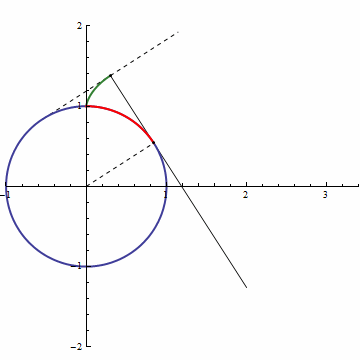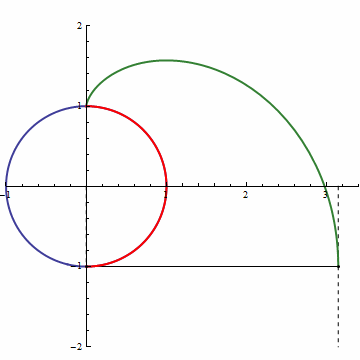
3、 把单位圆和渐开线画在一起，可以用Show，但这里推荐另一个命筠沭鱿漆令函数Graphics，因为它会自动忽略坐标轴。 先把图形转换成数据，运行下面的代码：单位圆 = P锾攒揉敫arametricPlot[{Sin[x], Cos[x]}, {x, 0, 2 Pi},PlotStyle -> {Thick, Red}][[1]];渐开线 = ParametricPlot[{Cos[t] + t Sin[t], Sin[t] - t Cos[t]}, {t, 0,6 Pi}, PlotStyle -> {Thick, Blue｝][[1]]; 再用Graphics统一绘图：Graphics[{单位圆, 渐开线｝]

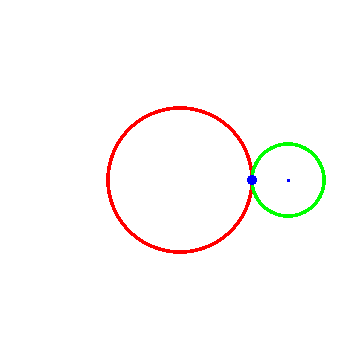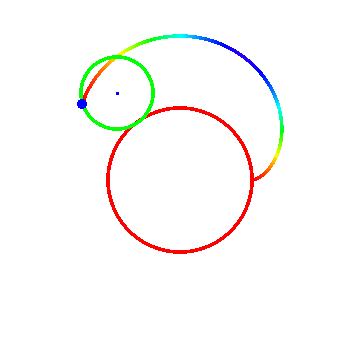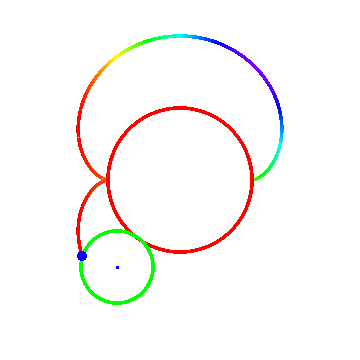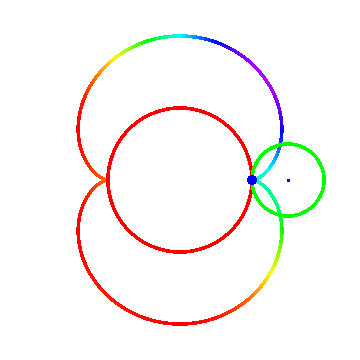
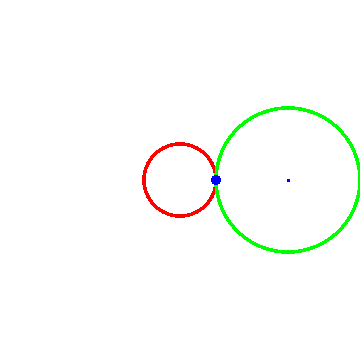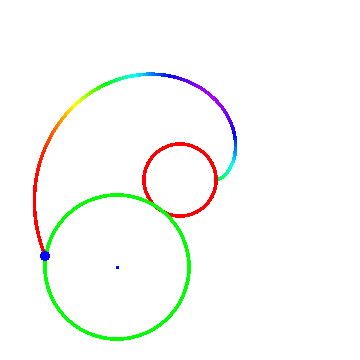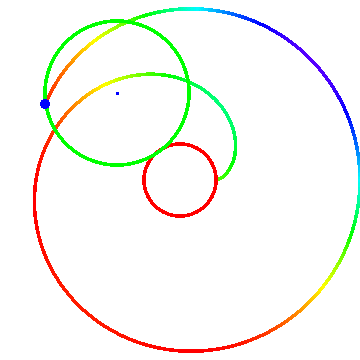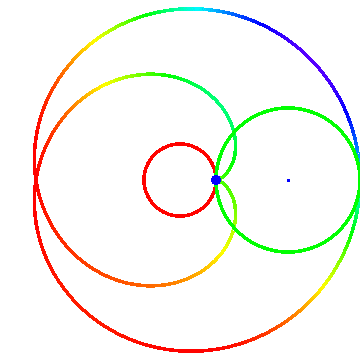
2、 把不同的情形，各导出个动态图： 图一里面R = 1， r = -1; 图二里面R = 2， r = -1; 图三里面R = 1 ，r = -2。 其余的，大家可以自己尝试。要注意参数的范围！代码在动态图后面的后面！

外摆线的拓广

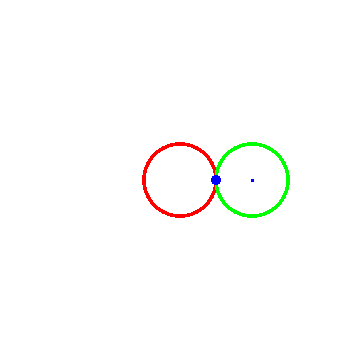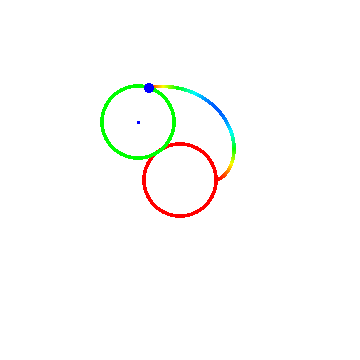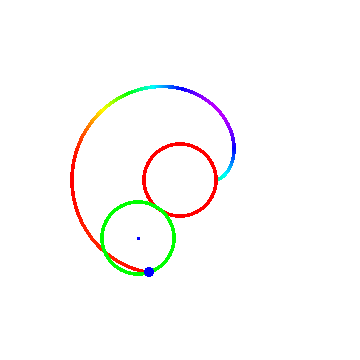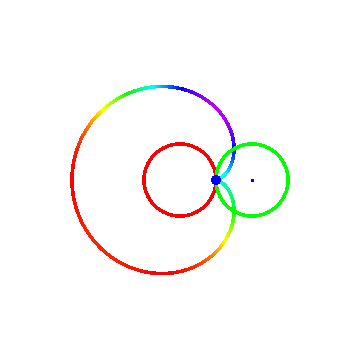
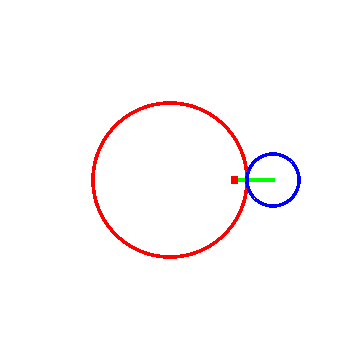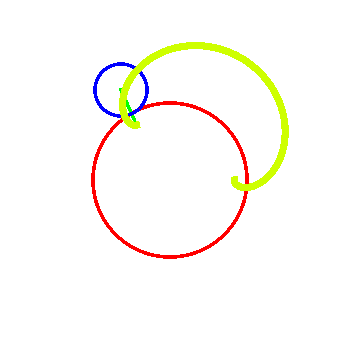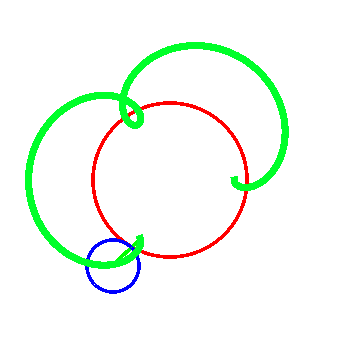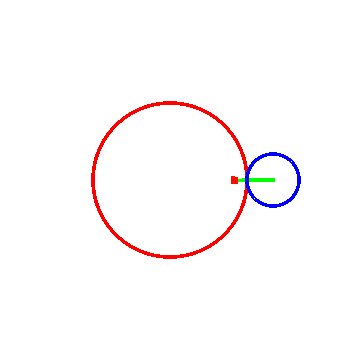
1、 如果“被追踪点”位于圆A的内部或外部，那么它在时间t的位置坐标需要重新下定义，同时还要引进一个参数d（“被追踪点”到圆A的圆心的距离）：pt[t_, r_, d_] :=lctr[t, r] + RotationMatrix[2 Pi - t/r].{d r Cos[t/R], d r Sin[t/R]} 其中，d>0且d≠1。 代码在动态图里面，注意代码里的Abs[r]。