怎么证圆周角是圆心角的一半

1、首先，我们要知道圆的基本定义。在同一平面内，到定点的距离等于定长的点的集合叫做圆。这个定点叫做圆的圆心，定长是圆的半径。所以，圆上所有点到圆心的距离都相等。

2、在这个证明过程中需要用到的知识点：（1）圆的定义：圆上所有点到圆心的距离都相等，（2）等腰三角形两底角相等，（3）三角形的外角等于不相邻的两个内角之和

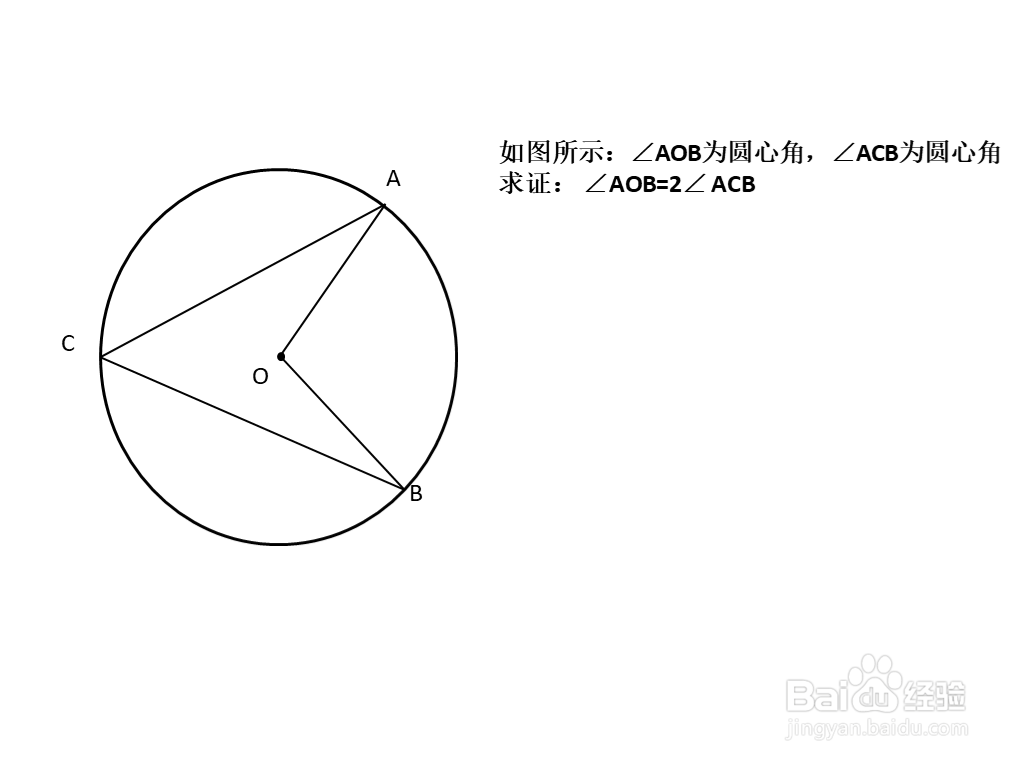
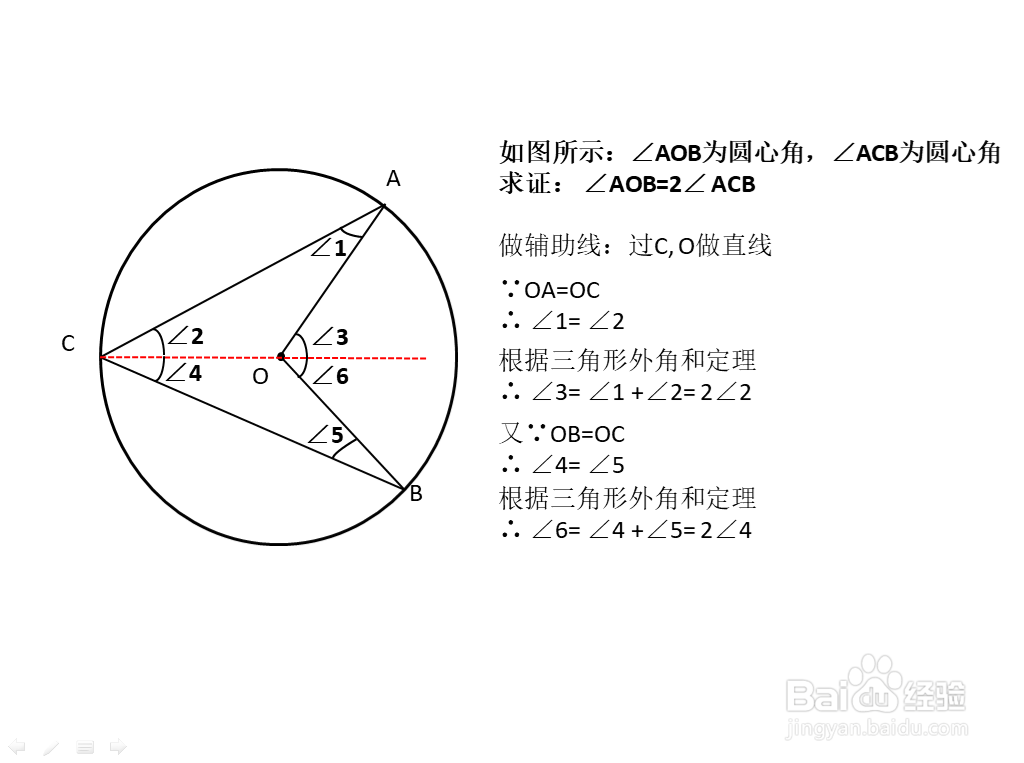
3、如图所示，∠AOB为圆心角，∠ACB为圆心角

求证： ∠AOB=2∠ ACB

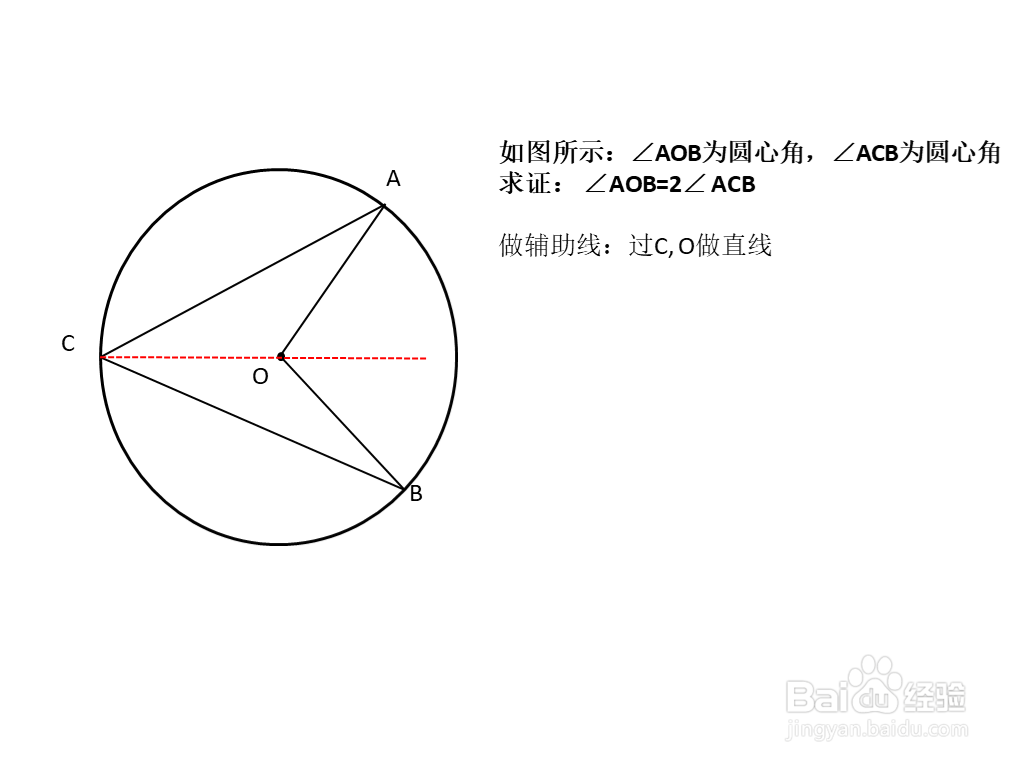
4、证明过程如下：首先，做辅助线，连接C, O画一条直线

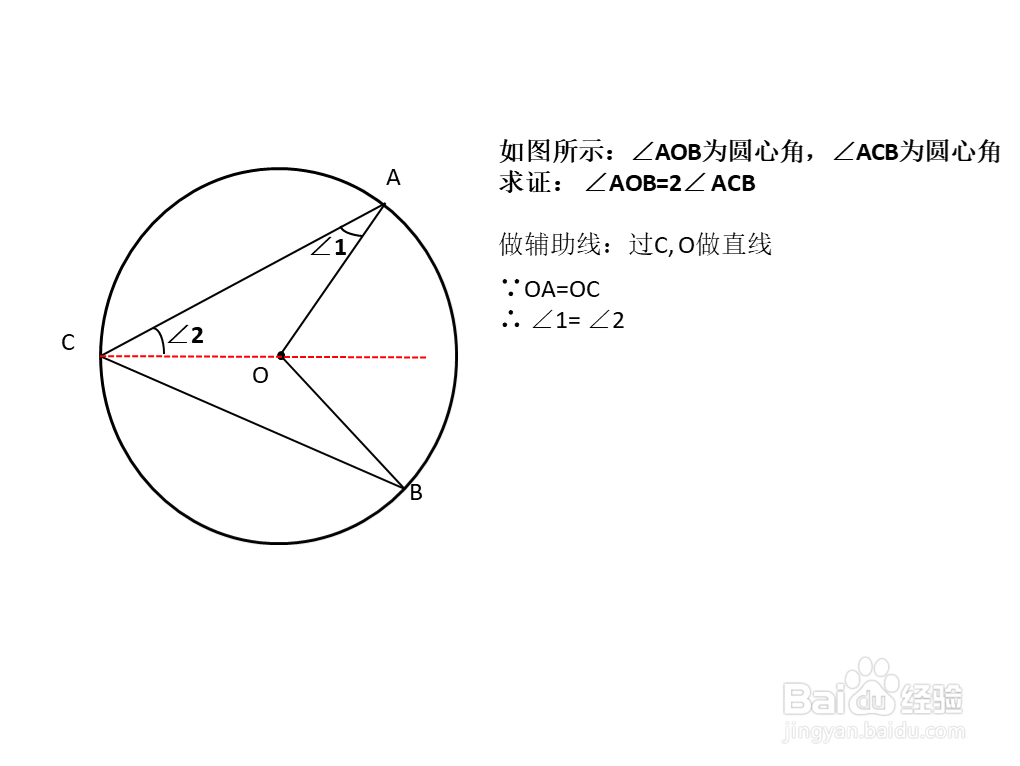
5、∵OA=OC

∴ ∠1= ∠2

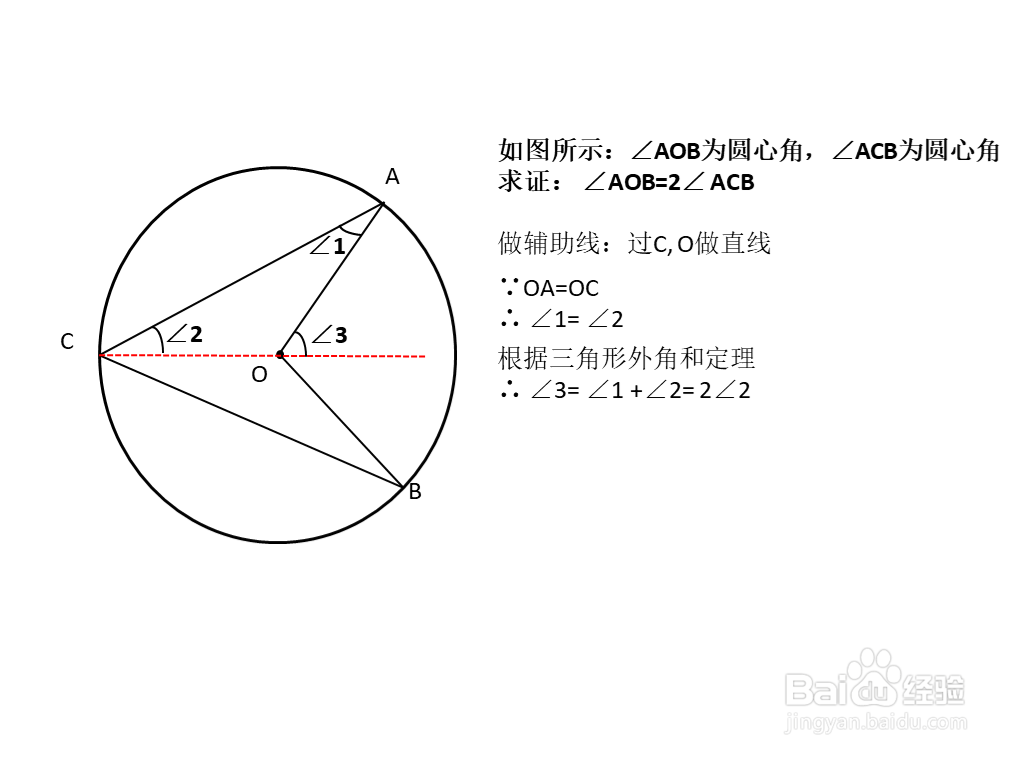
6、根据三角形外角和定理

∴ ∠3= ∠1 +∠2= 2∠2

7、又∵OB=OC

∴ ∠4= ∠5

根据三角形外角和定理

∴ ∠6= ∠4 +∠5= 2∠4

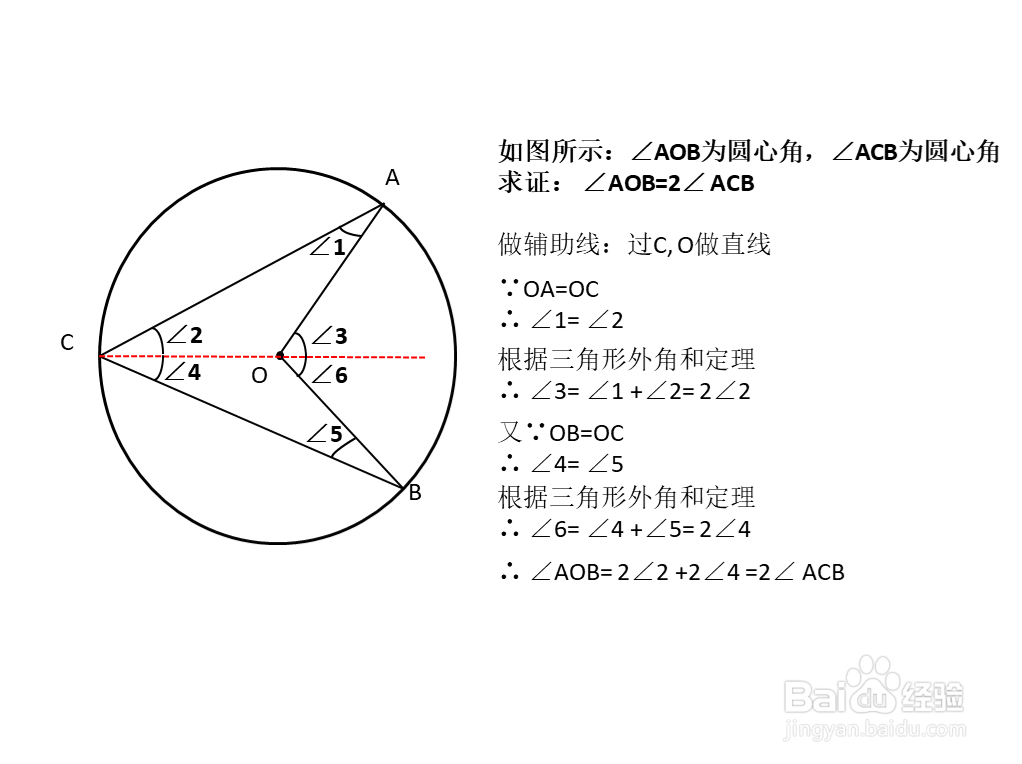
8、∴ ∠AOB= 2∠2 +2∠4 =2∠ ACB