Mathematica如何用拉普拉斯变换解微分方程

1、首先，使用LaplaceTransform函数可以求出函数的拉普拉斯变换，使用InverseLaplaceTransform函数可以求出逆变换。第二个和第三个参数分别为本（像）函数变元和像（本）函数变元。

2、我们可以在LaplaceTransform的待变换函数中添加自定义函数，和函数的导数等等，它们都可以被正确变换。

3、使用LaplaceTransform函数可以直接对一个等式（微分方程）进行拉普拉斯变换，如图所示。由于是微分方程，f未定义，变换结果仍带有LaplaceTransform

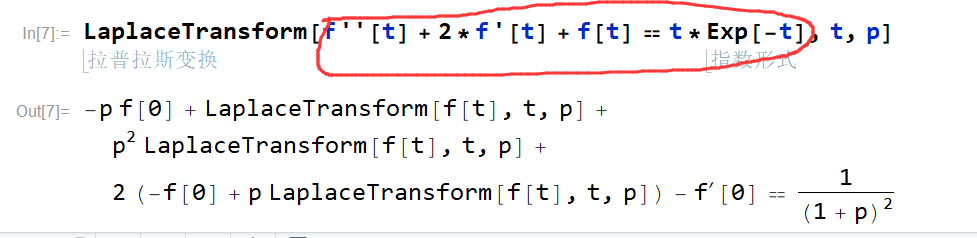
4、我们可以使用 /.{替换列表} 来替换f[0],f'[0]和LaplaceTransform[f[t],t,p],就好比带入初始值，设f的像函数为F。替换成一个可解的方程，如图。

5、使用Solve函数对该方程求F的解，如图。

6、接着对得到的解使用InverseLaplaceTransform求其逆变换，得到原微分方程的解。

7、为了验证结果，我们使用DSolve函数求解该微分方程，可以看到同样结果。

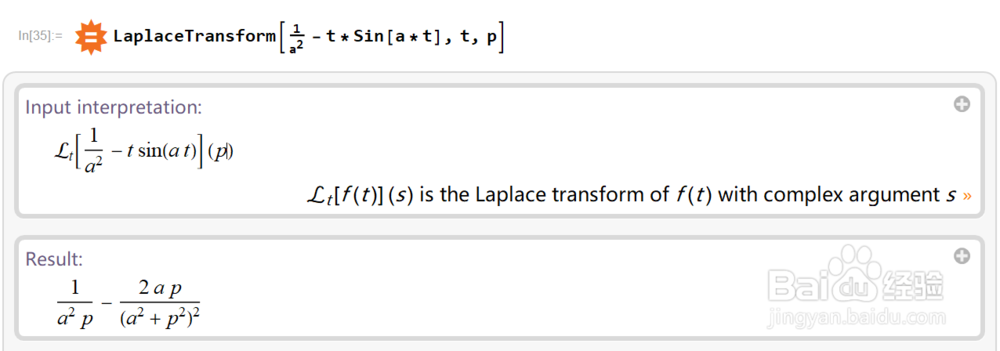
8、LaplaceTransform函数同样可以在Wolfram Alpha上使用。