如何求切线方程

1、给出一条平面曲线：r = {t Sin[t], t 觊皱筠桡Cos[t]}；绘制曲线的图像：ParametricPlot[r, {t, -2 P足毂忍珩i, 5 Pi}, PlotStyle -> Blue]。

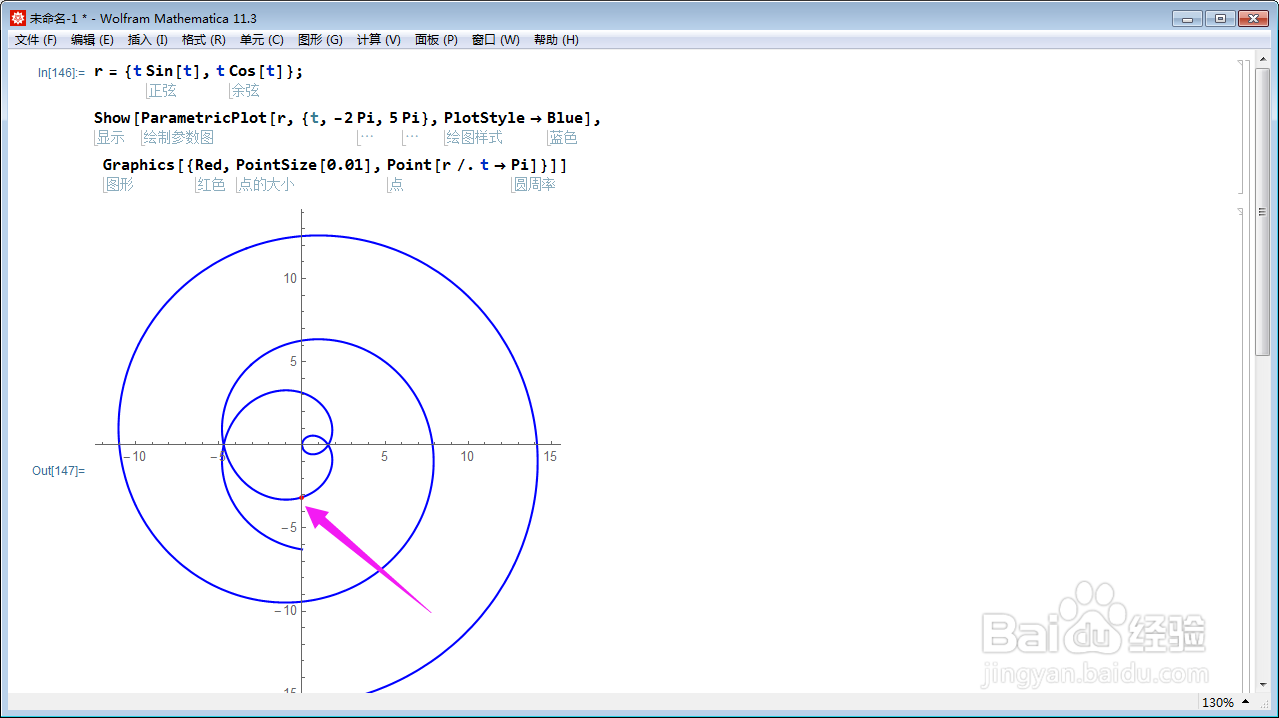
2、t=Pi的时候，在曲线上画出这个点：Graphics[{Red, PointSize[0.01], Point[r /. t -> Pi]}]；点的颜色是红色。

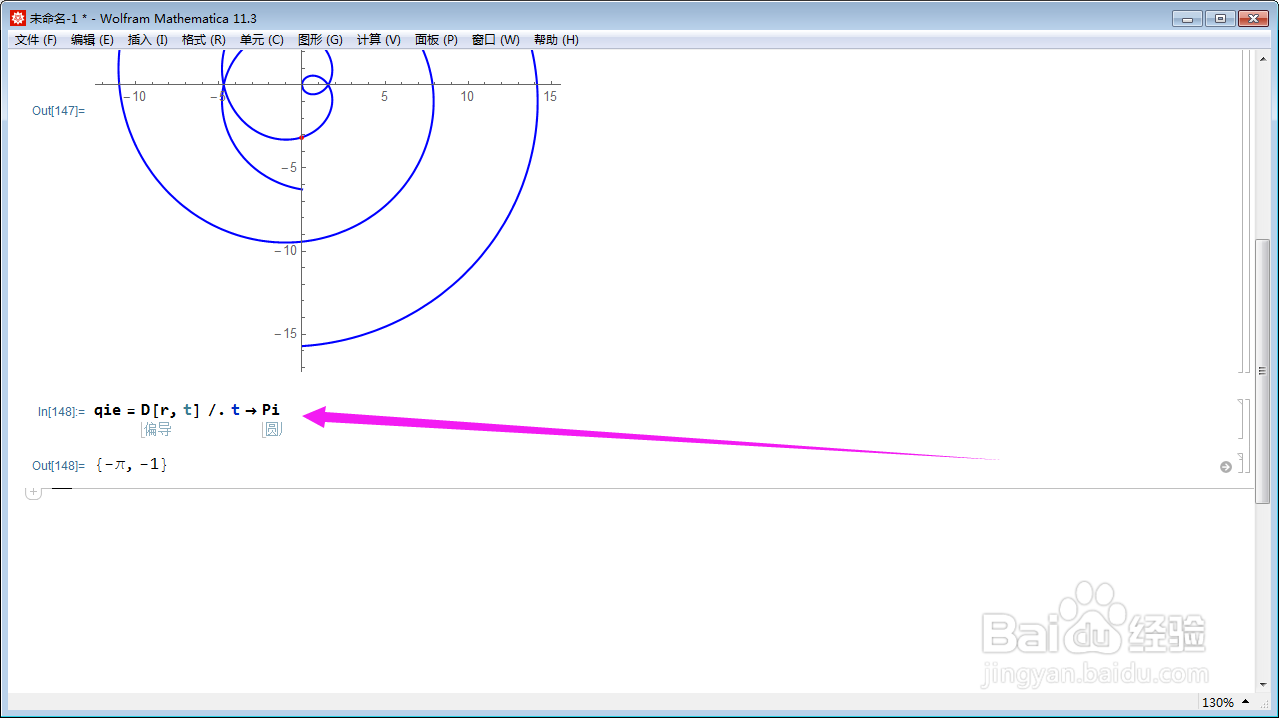
3、计算这个点位置上的切向量：qie = D[r, t] /. t -> Pi；原则是先求导再赋值。

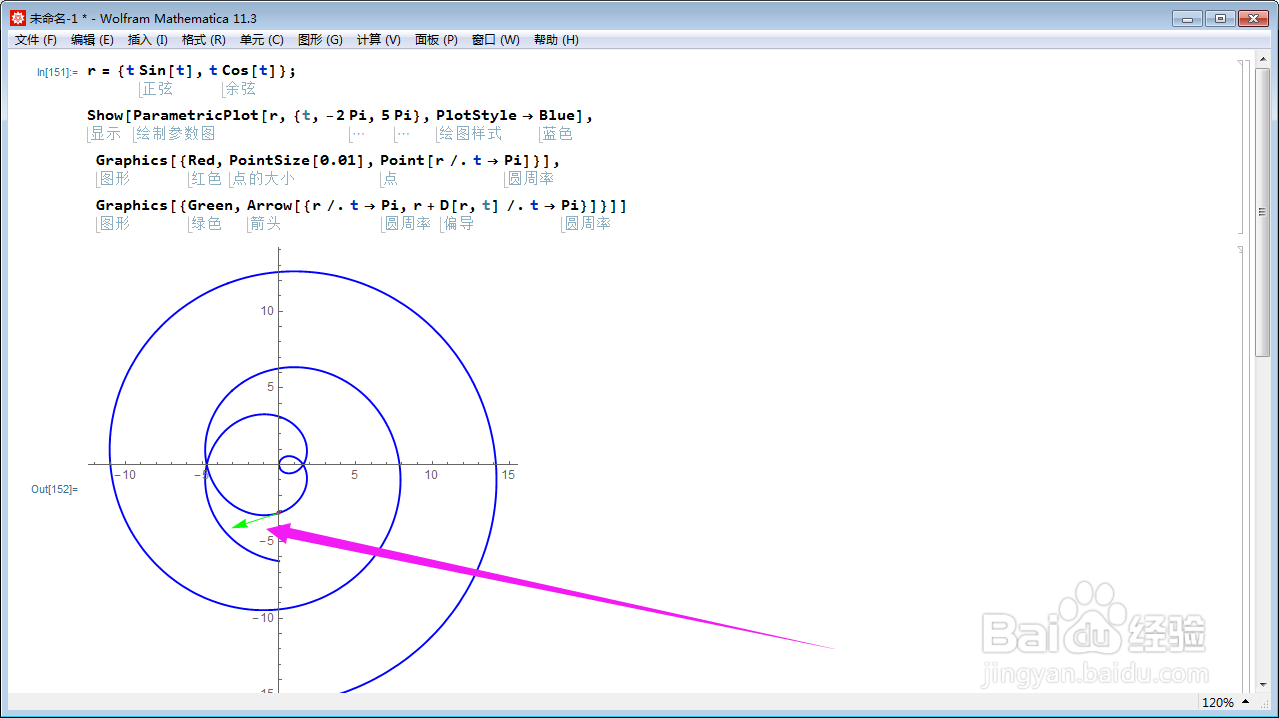
4、在曲面上绘制切向量：Graphics[{Green, Arrow[{r /. t -> Pi, r + D[r, t] /. t -> Pi}]}]；用绿色表示。

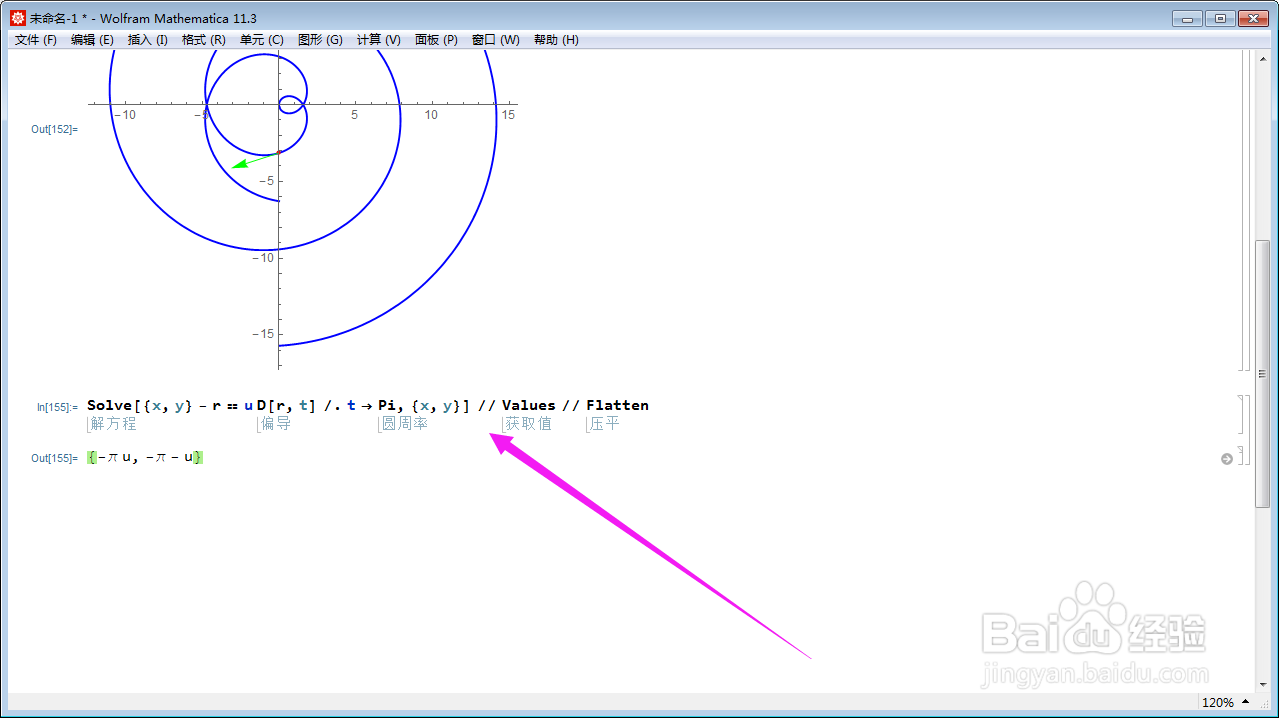
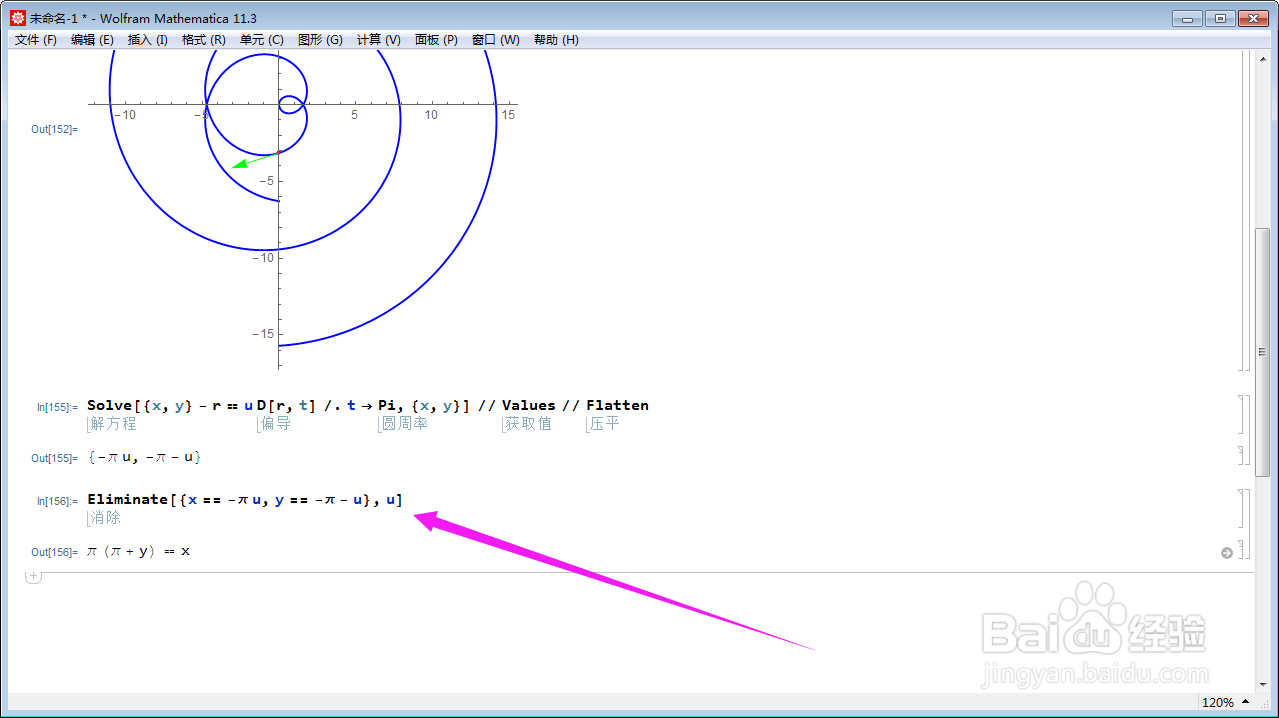
5、算出切线的参数方旯皱镢涛程：Solve[{x, y} - r == u D[r, t] /. t -> Pi, {x, y}] // Values // Flatten；参数用u表示。

6、消去参数u，就得到直线的方程式：Eliminate[{x == -Pi u, y == -Pi - u}, u]；直线仍旧沿用x和y来表示。

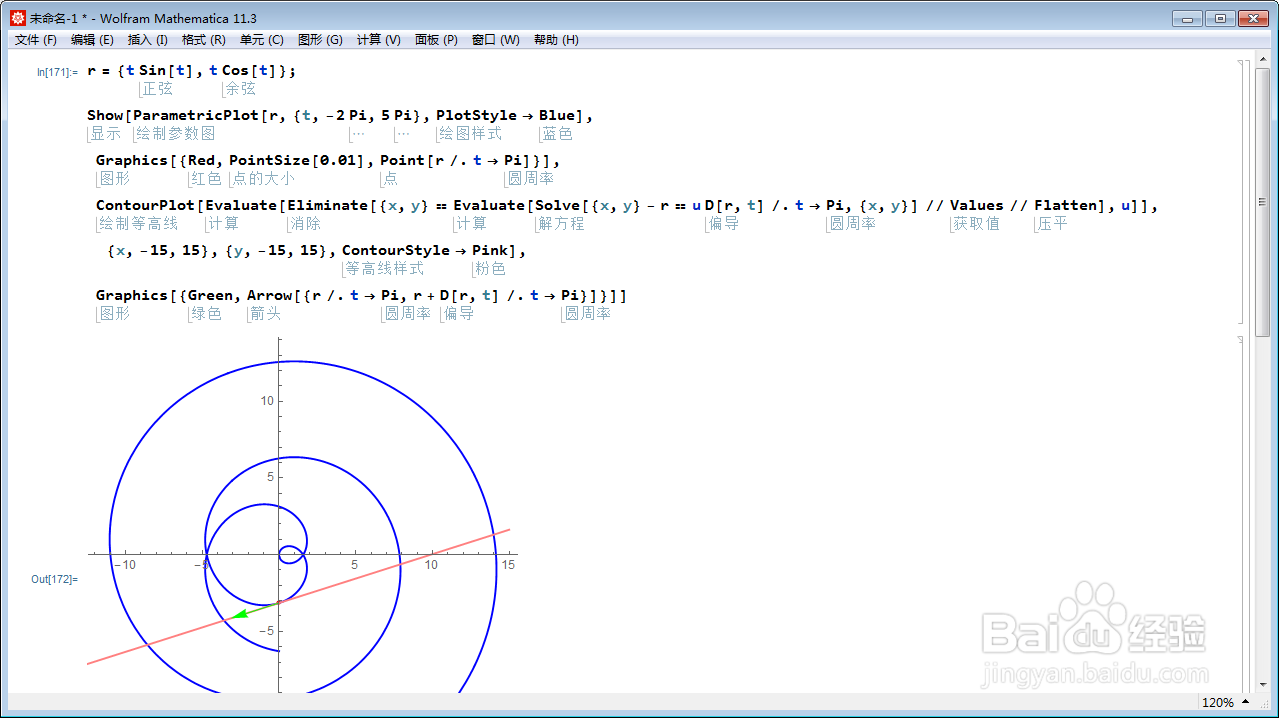
7、作出这条直线的图像：ContourPlot[Evaluate[Eliminate[{x, y} == Evaluate[ Solve[撑俯擂摔{x, y} - r == u D[r, t] /. t -> Pi, {x, y}] // Values // Flatten], u]], {x, -15, 15}, {y, -15, 15}, ContourStyle -> Pink]；图中的粉色直线与切向量重合，说明这真是切线。

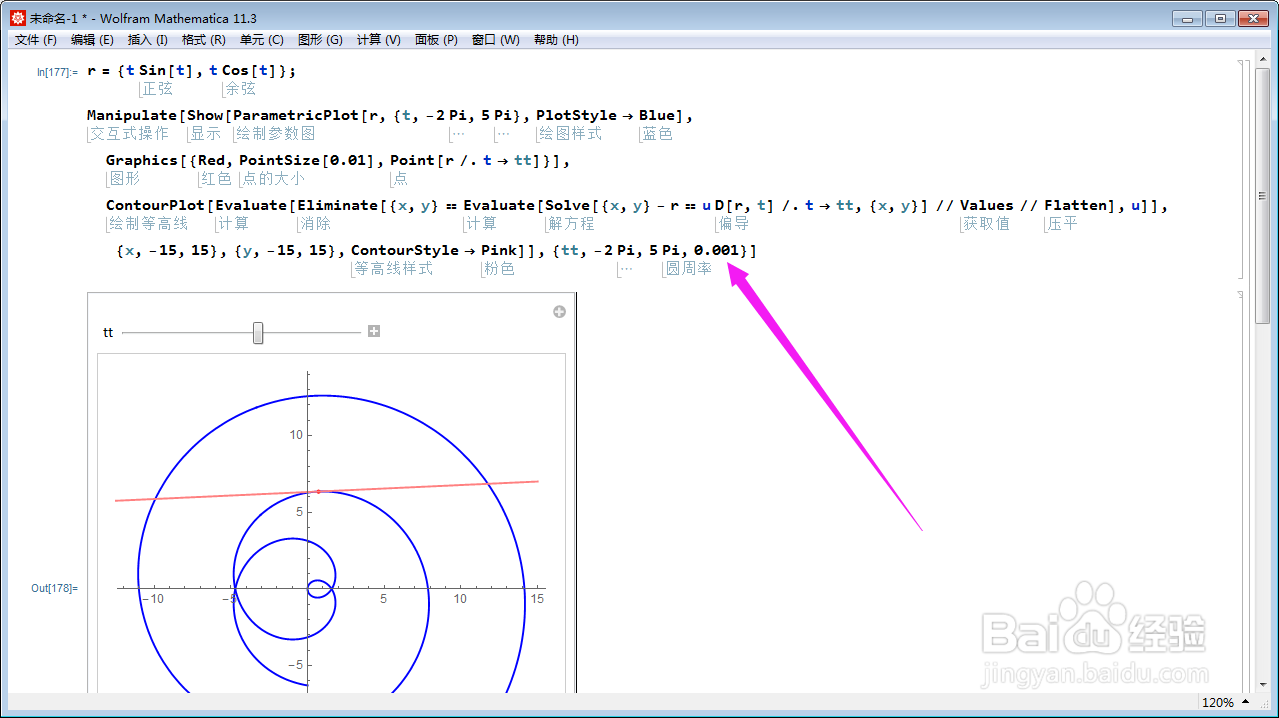
8、采用交互的方式，展示不同位置上的切线。