如何用geogebra5求解线性规划问题解.docx
1、线性规划模型的数学模型都有着共同的特征,它们都是要求一组变量,一般是(非负的)在一组线性的约束条件下,使得一个线性的目标函数取得最大值或最小值,我们把这类问题统称为线性规划问题,根据问题的性质,线性规划有多种形式,目标函数有要求最大化的!也有要求最小化的,约束条件可以是不等式,也可以是等式,决策变量一般是非负的"因此,我们可以抽象出线性规划的一般形式:

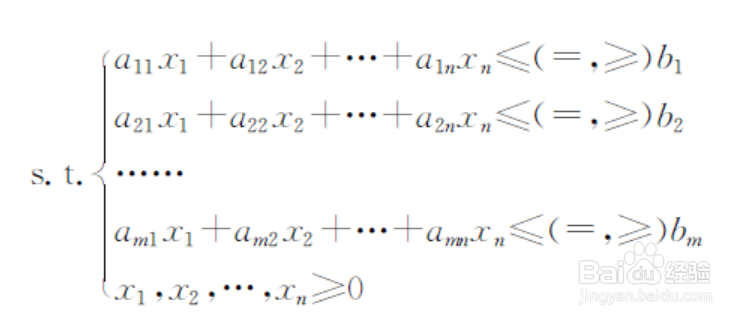
2、其中:我们要达到的最大化或最小化的目标式称为目标函数,下边的方程组称为约束条件(s.t.),表明在规划中将要受到的资源限制,求出的使目标达到最优的,x1到xn的取值叫做最优解,把最优解代入目标函数求出的目标函数值称为最优值。
线性规划的研究对象是稀缺资源最优分配问题,即将有限的资源以最佳的方法,分配于相互竞争的活动之中,一般体现为在一定的资源条件下,如何合理使用,达到效益的最大化,或者在给定任务下,如何统筹安排,尽量降低成本,使资源消耗最小化,由于这些问题从本质上看很多都是线性的,所以我们称之为线性规划。
1、在建立了线性规划的模型之后,接下来就要求解模型了,在求解线性规划模型时,最简单的方法就是图解法,当线性规划问题中变量个数为2个时,我们可以在直角坐标系中把变量及其变化方向(范围)等用图直观地表示出来,从而求得目标函数的最佳取值,这种方法就是图解法,在应用中,图解法相对是比较缺乏实际意义的,但通过这种方法,可以形象地说明线性规划的许多特征,接下来,我们用图解法求解一个以下条件的模型:
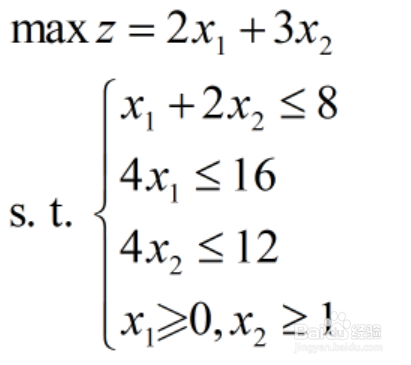
1、1.打开Geogebra,先利用所有约束条件绘制可行域(注意,在Ggeogebra中用自变量x代表模型中x1,y代表模型中x2).
在指令区域输入命令:
a: x + 2y ≤ 8 ∧ 4x ≤ 16 ∧ 4y ≤ 12 ∧ x > 0 ∧ y ≥ 1
∧ 表示“且”,可点右下角的 α 按钮,调出符号框,点击输入,输入完毕以后,按回车键,可以看到生成了一个由不等式条件的蓝色区域,如下图所示:
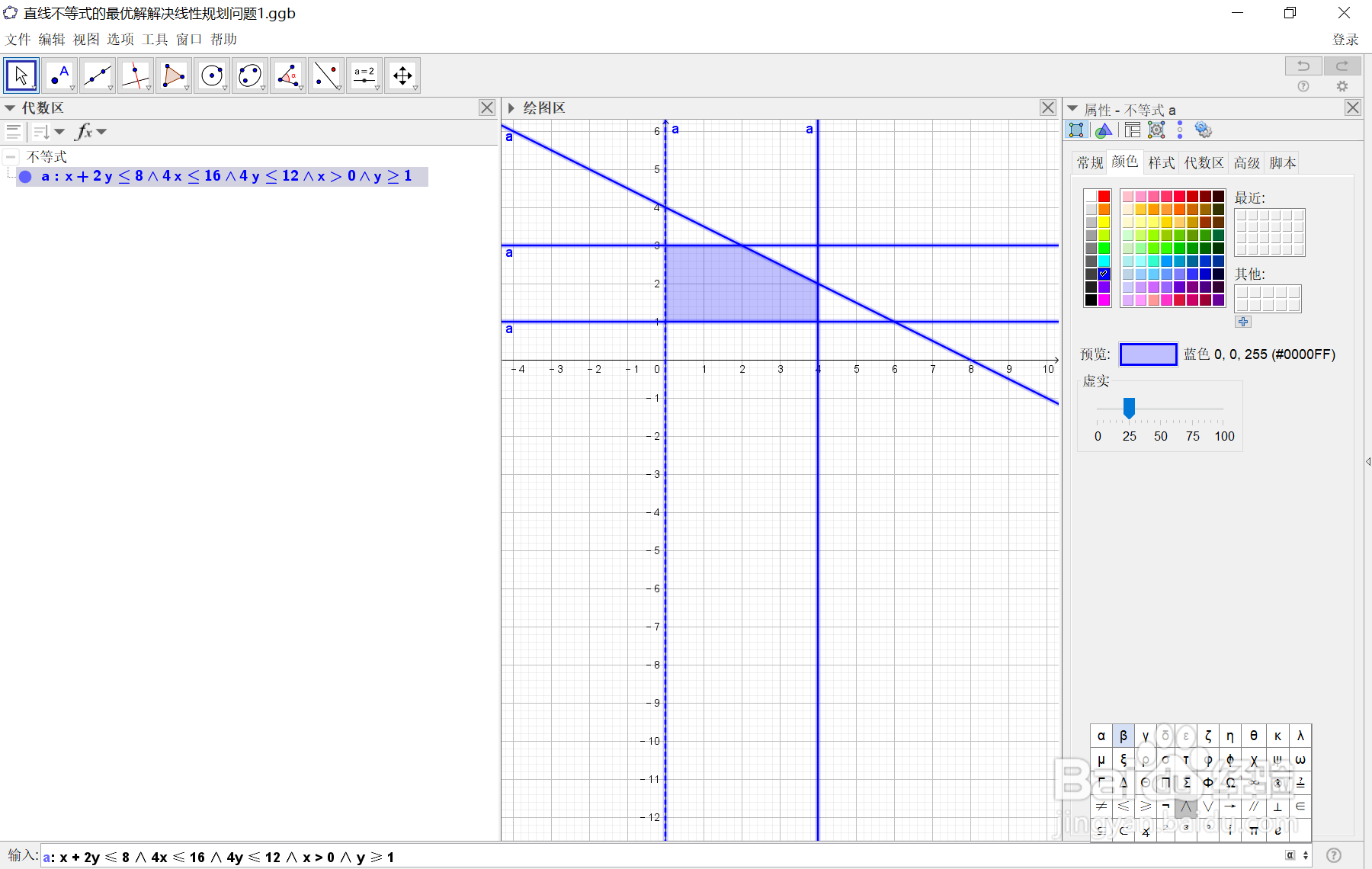
2、2.绘制目标函数max k=2x+3y的滑动直线,目标函数是一条直线,要让它动起来,用一个滑动条参数即可:
先点【滑动条】,设置参数名称为 k,最小输入【-5】,最大输入【20】(需要大概估计一下,或者后续再调整),增量输入【0.1】,【确定】,如下图所示:
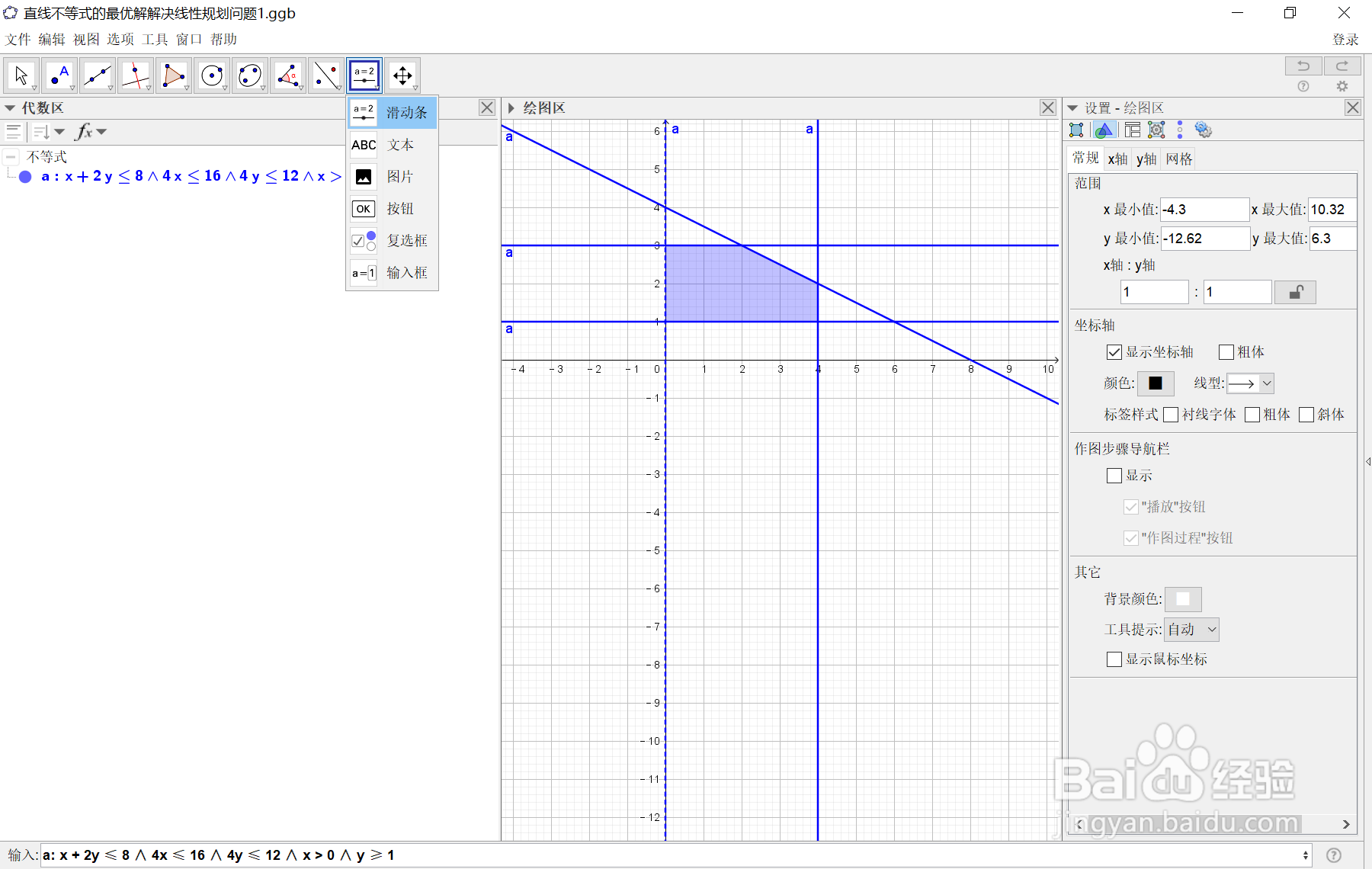
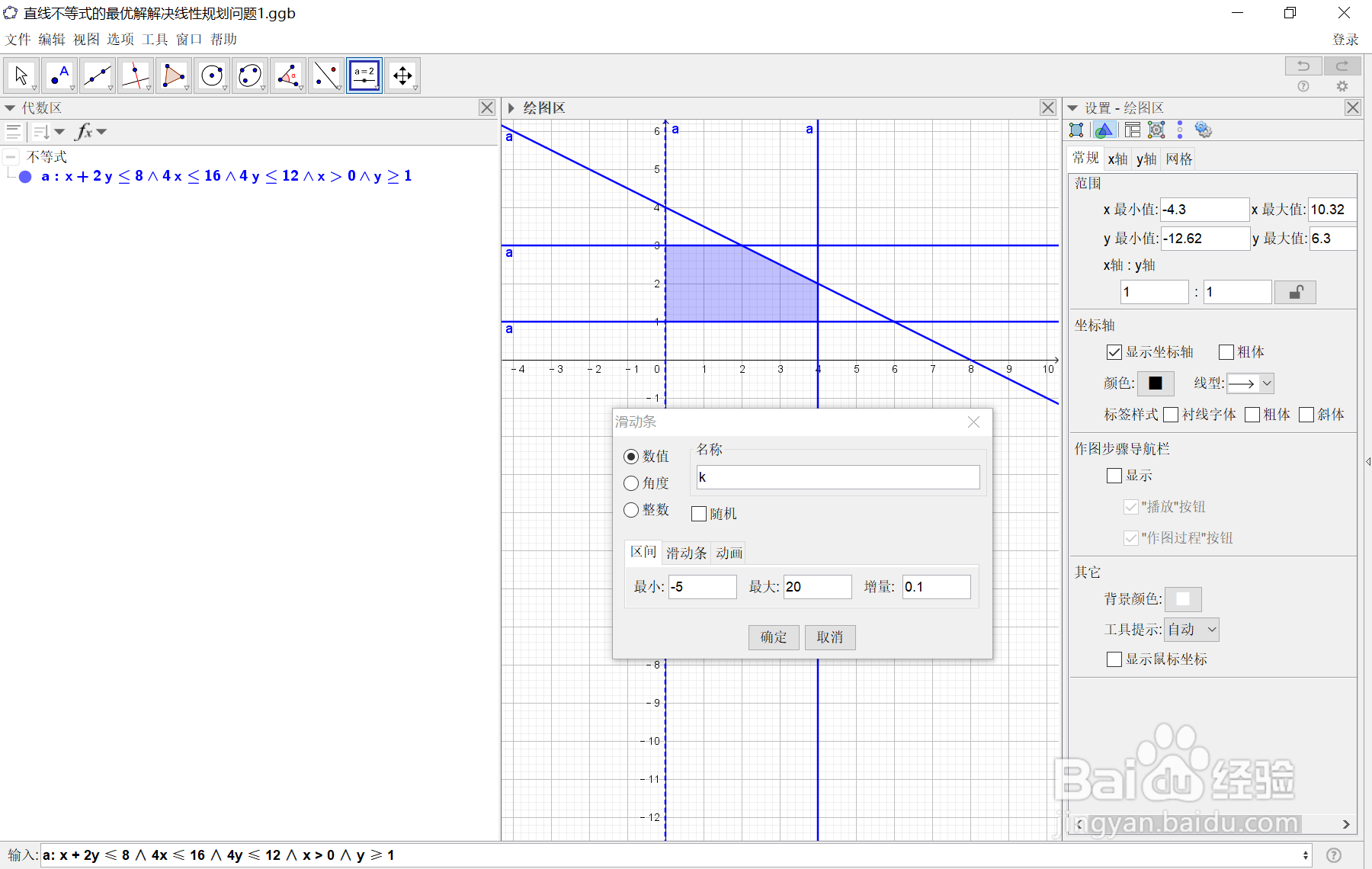
3、3.在指令区域输入命令:
b: 2x + 3y = k
此命令是用来求得目标函数z=2x+3y的最大值,其中图像中的黑色直线方程为:k=2x+3y=1,因为此时的 k值取默认的1,如下图所示:
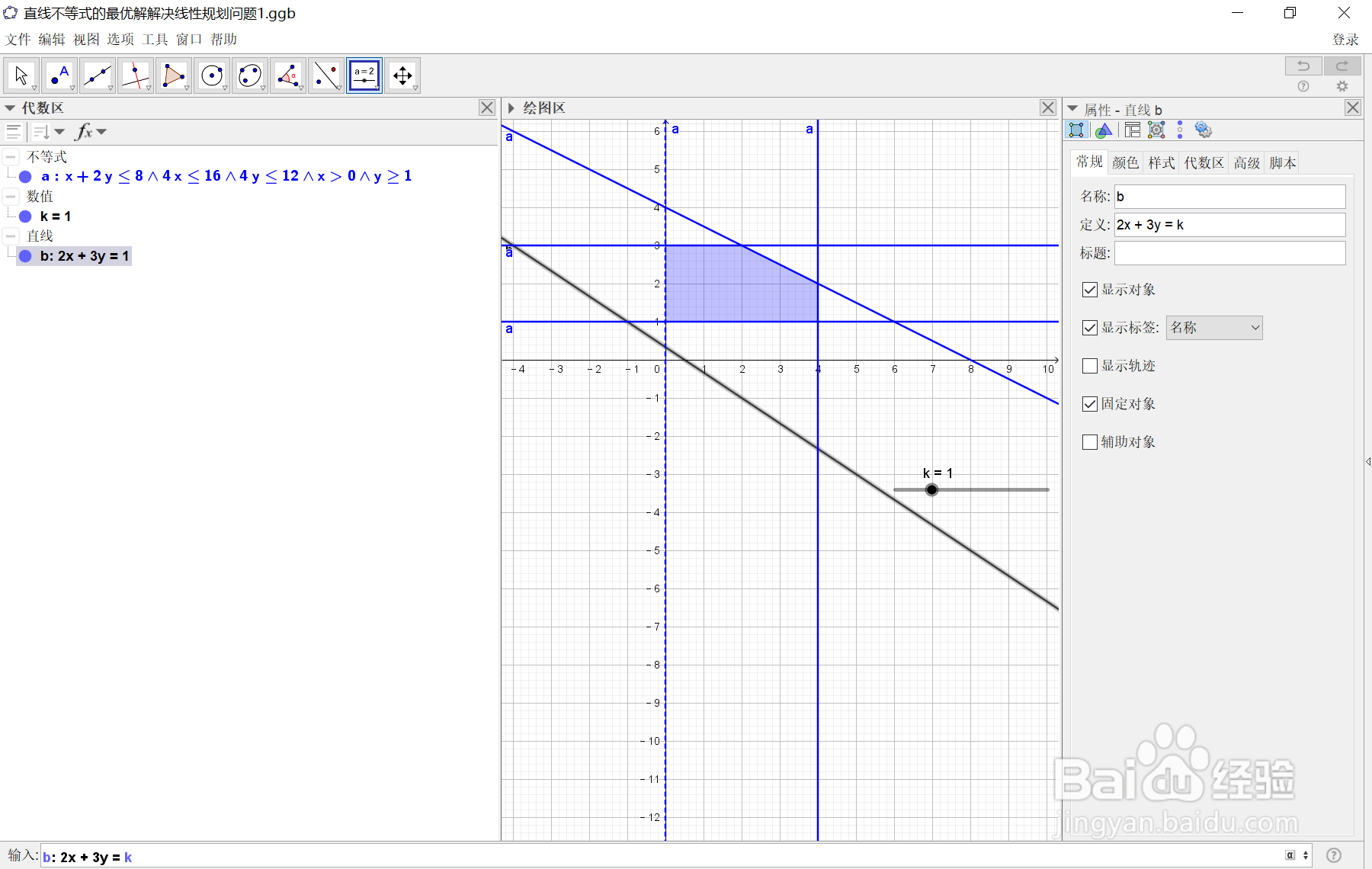
4、4.在指令区域输入命令:
c: x + 2y = 8
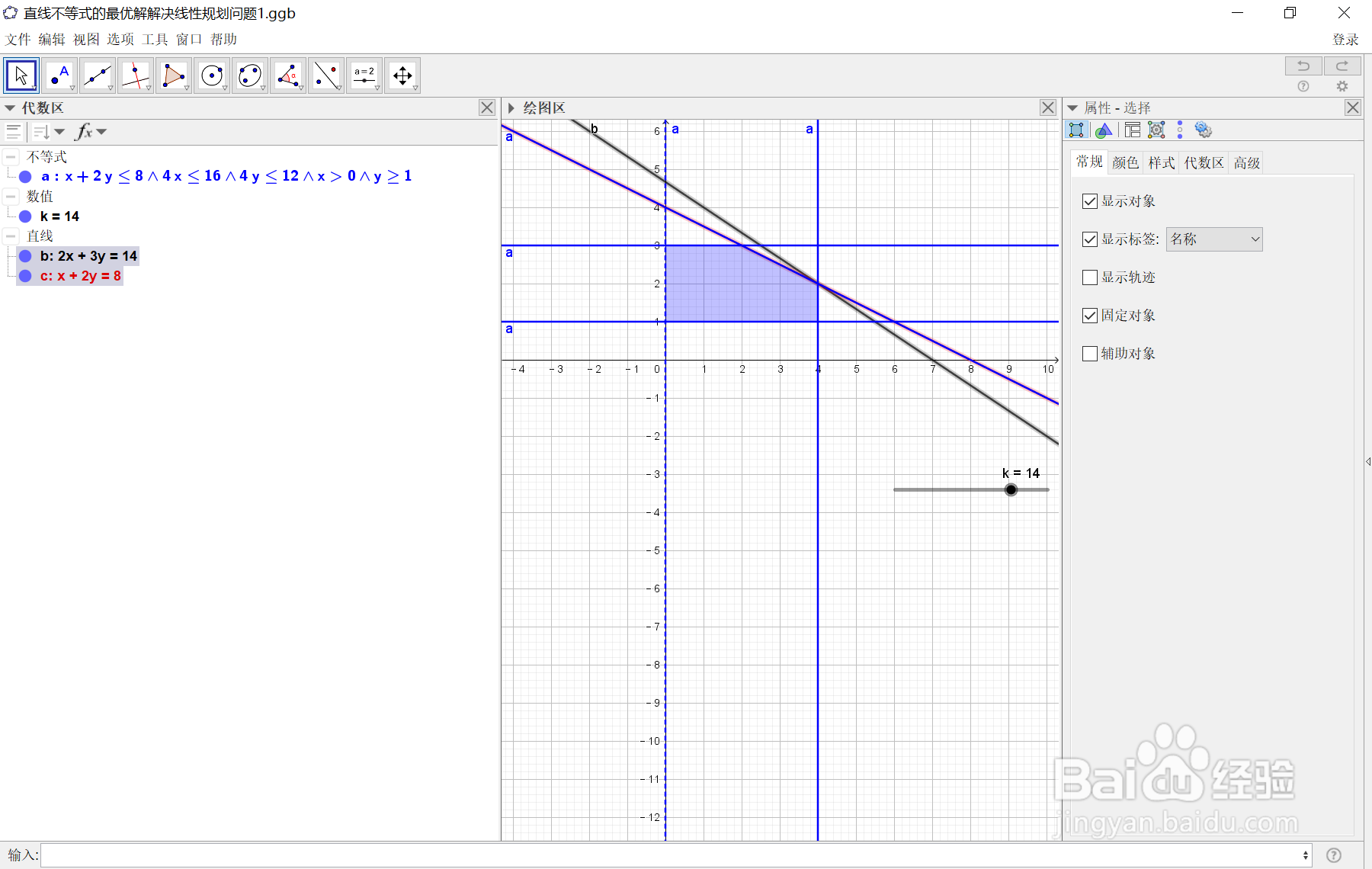
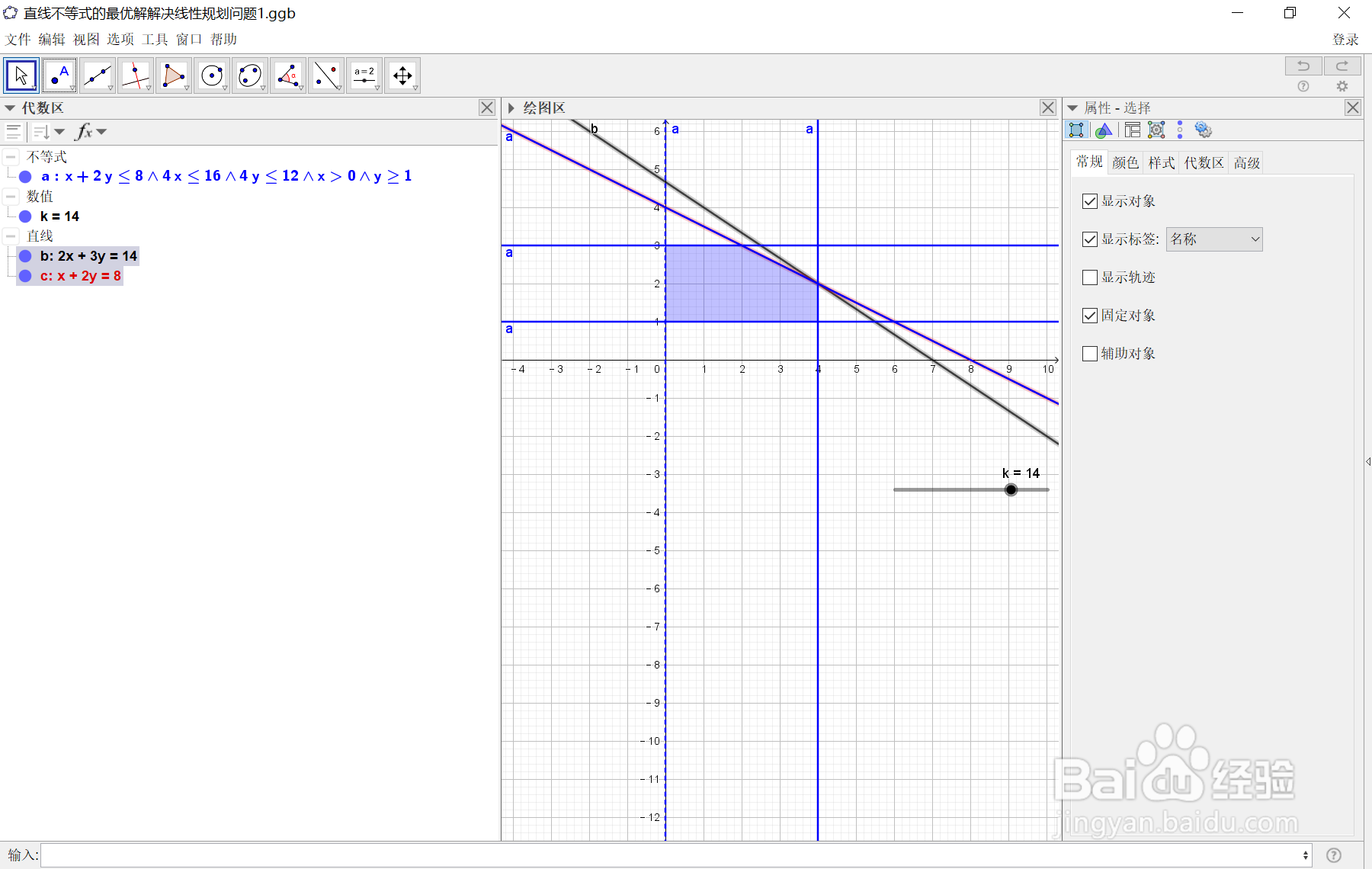
因为对于生成的不等式a的第一个约束条件(a: x + 2y ≤ 8 ∧ 4x ≤ 16 ∧ 4y ≤ 12 ∧ x > 0 ∧ y ≥ 1)为x + 2y ≤ 8,取临界值的方程为: c: x + 2y = 8,这样子做的目的就是为了求得此条直线与其它直线的交点,以便于我们分析目标函数z=2x+3y的最大值.为了区别于阴影部分的直线重叠,我们可以在代数区,先选中直线c: x + 2y = 8,然后将它的颜色更改为红色,操作过程如下图所示:
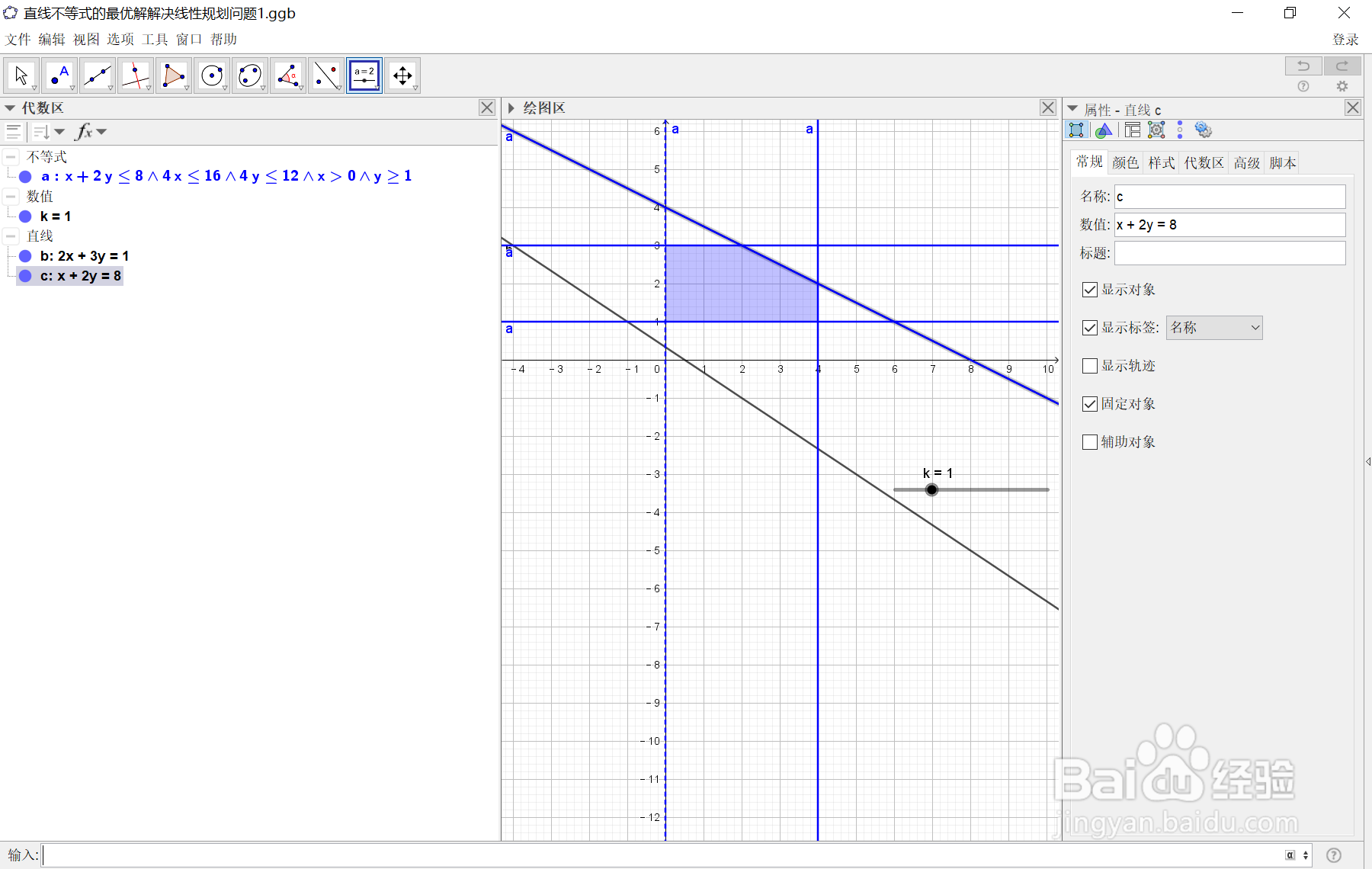
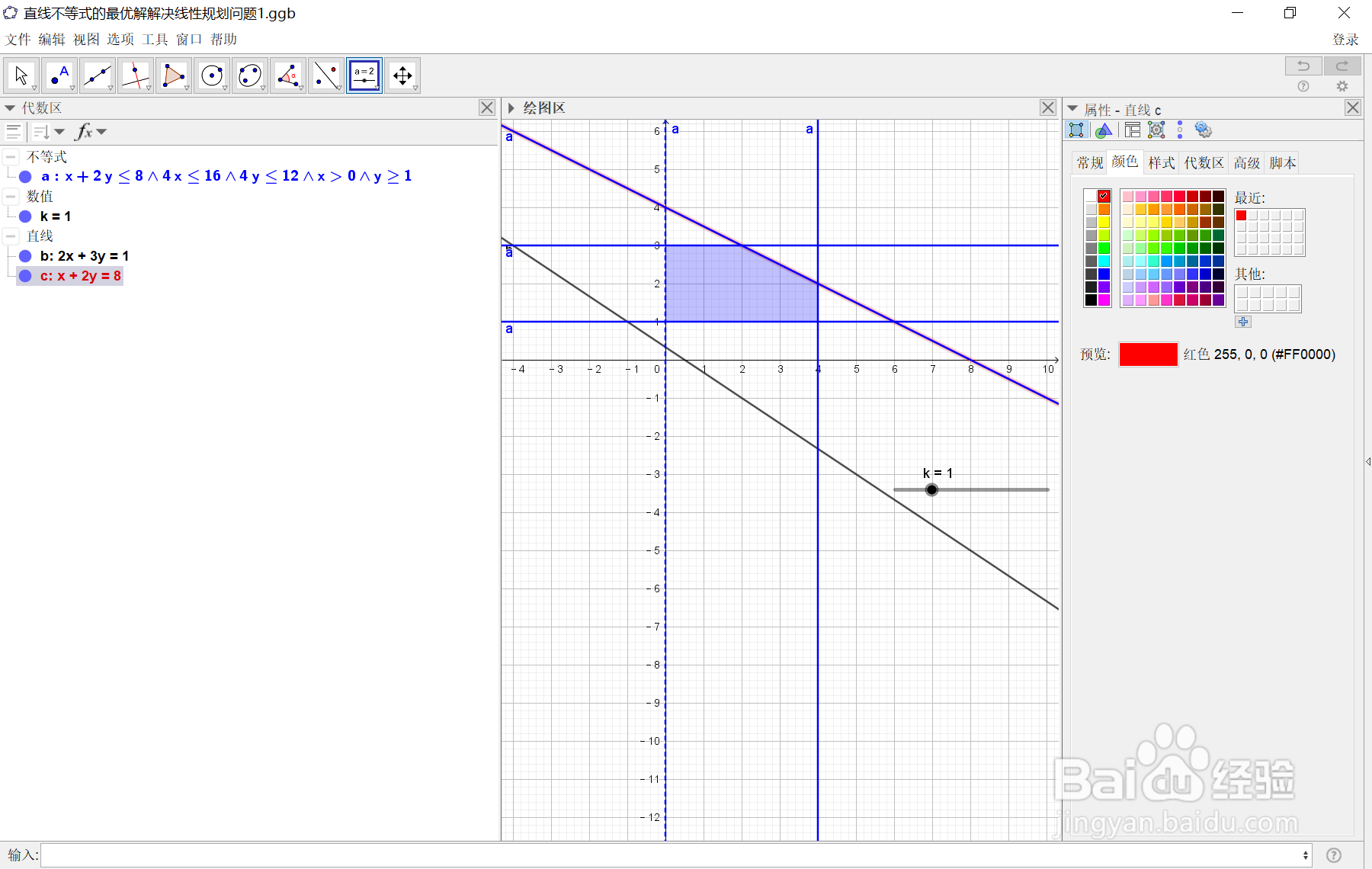
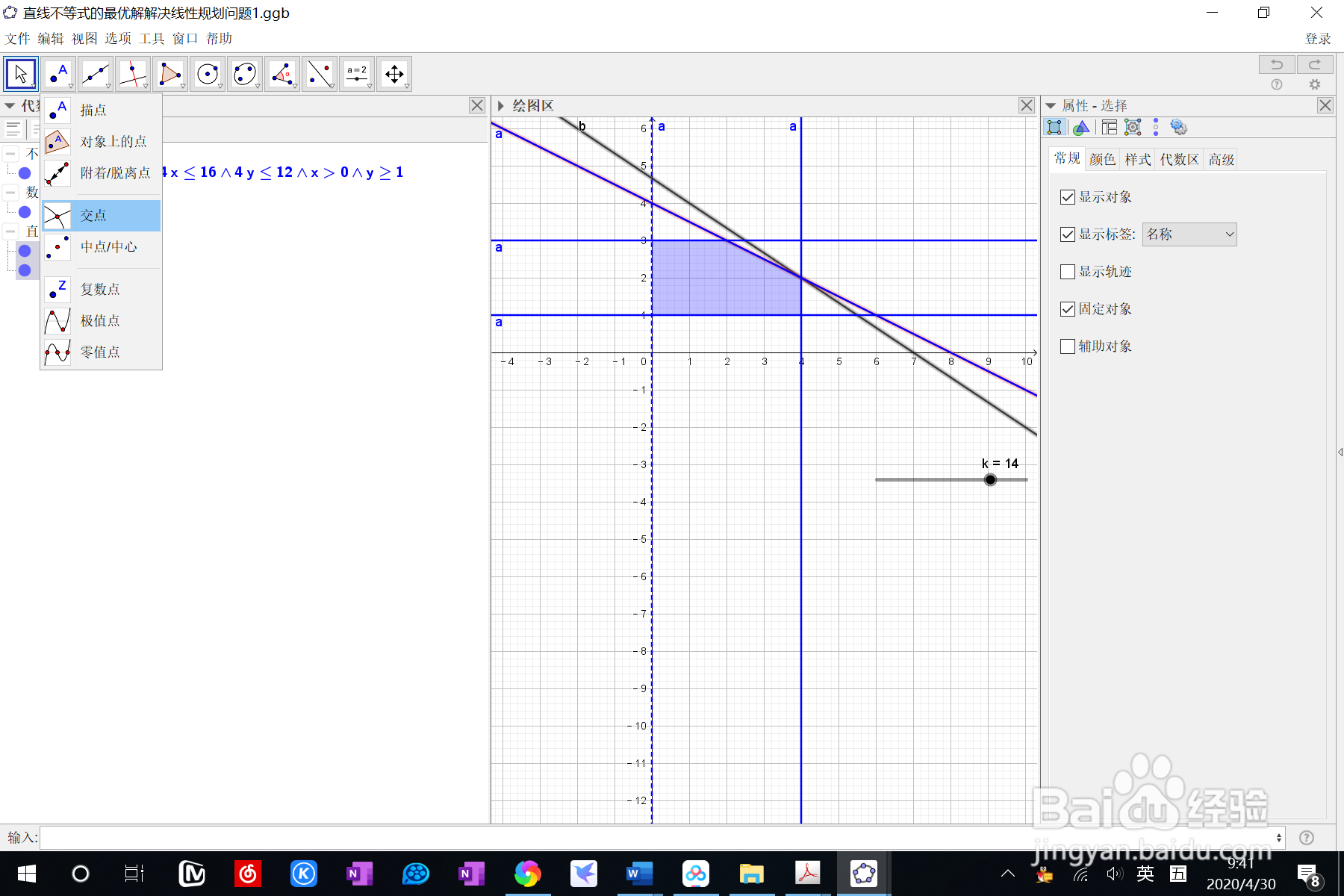
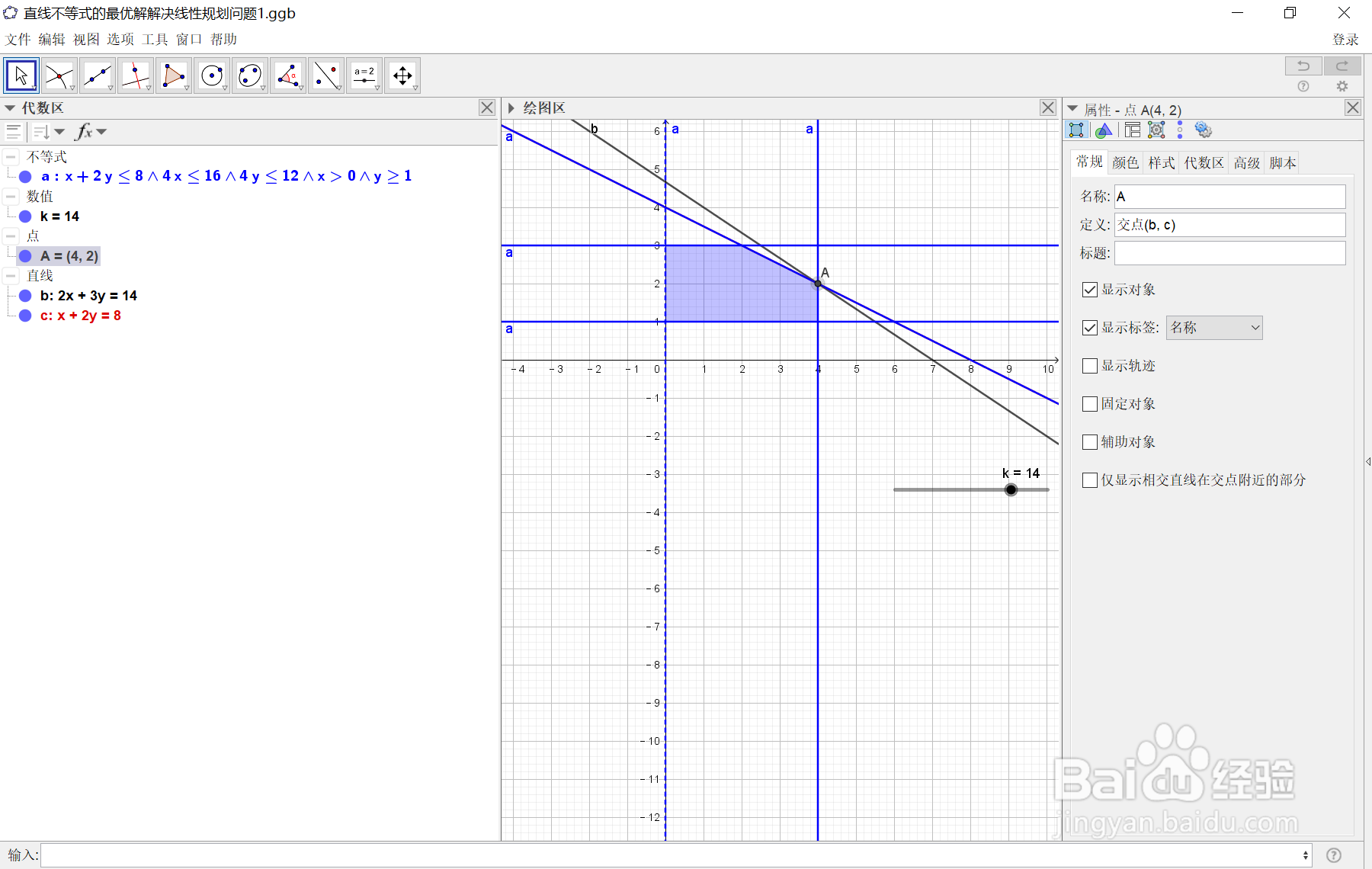
5、5:经过计算,将k的值调整到k=14,可以看到直线:b,c已经完全重合,这样做的目的是为了求出两直线的交点A的坐标,为考察目标函数k=2x+3y的最大值做准备.选在代数区按下ctrl键选中表达式b,c,然后选两直线交点,求得交点A的坐标为A=(4,2)操作过程如下图所示:
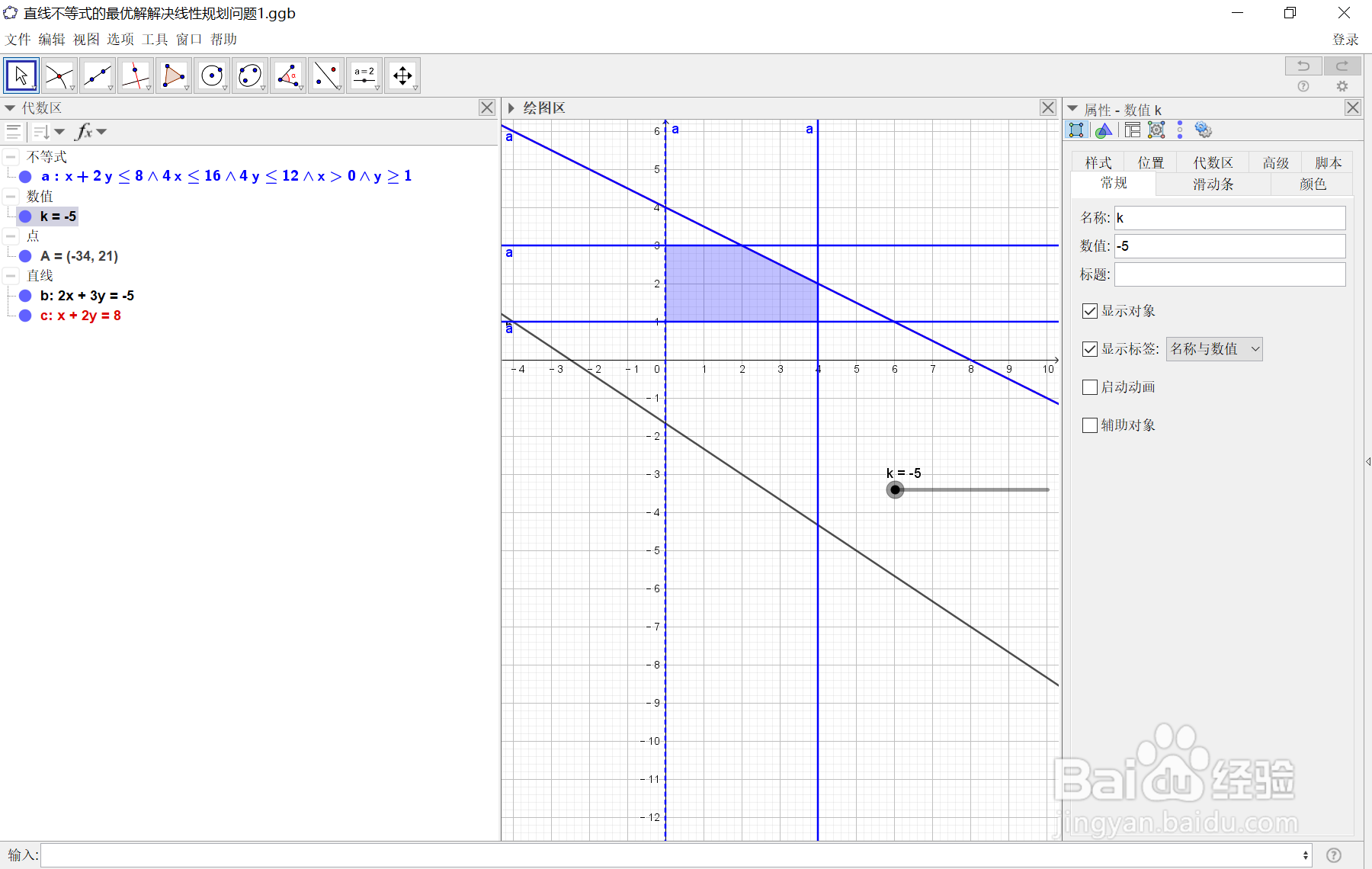
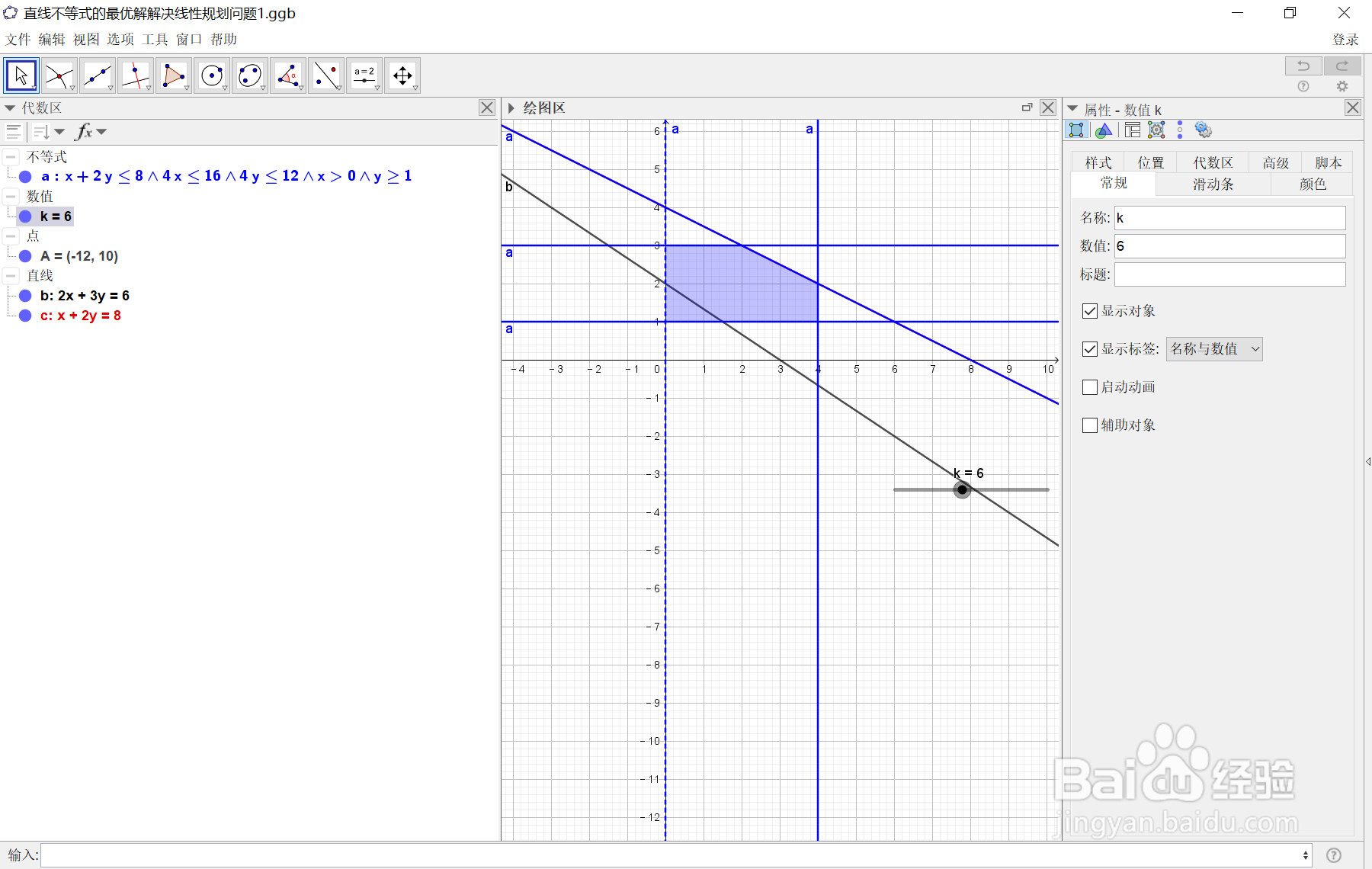
6、 现在,将k的值设置为我们自行设定的范围:-5到20,然后我们要在这个可行域中求得一个使目标函数达到最大的点!其实也就是说,当目标函数z=0时,作出目标函数的一条直线,在这条直线上,决策变量x1,x2的任何取值!对应目标函数z的取值都相等,我们把这条直线叫做等值线随着k的增大,直线一直向右平移,当直线平移到刚好要离开阴影部分的临界点时,再向右平移就与可行域没有交点了,这时就得到了的最大化目标值,如下图所示:
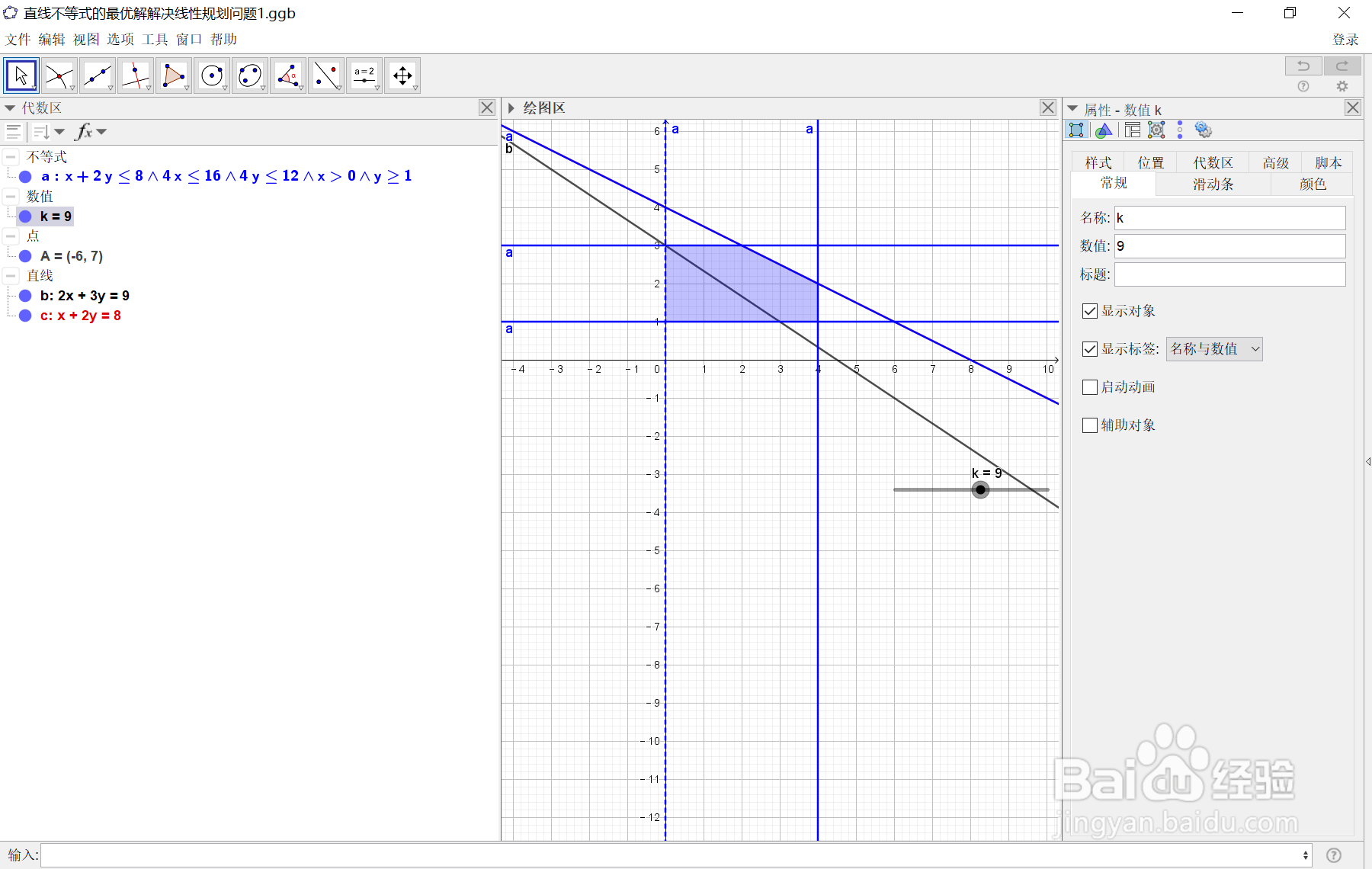
7、在调整k值的过程中,当k=13时,可以看到b,c两交点A出现,如下图所示:
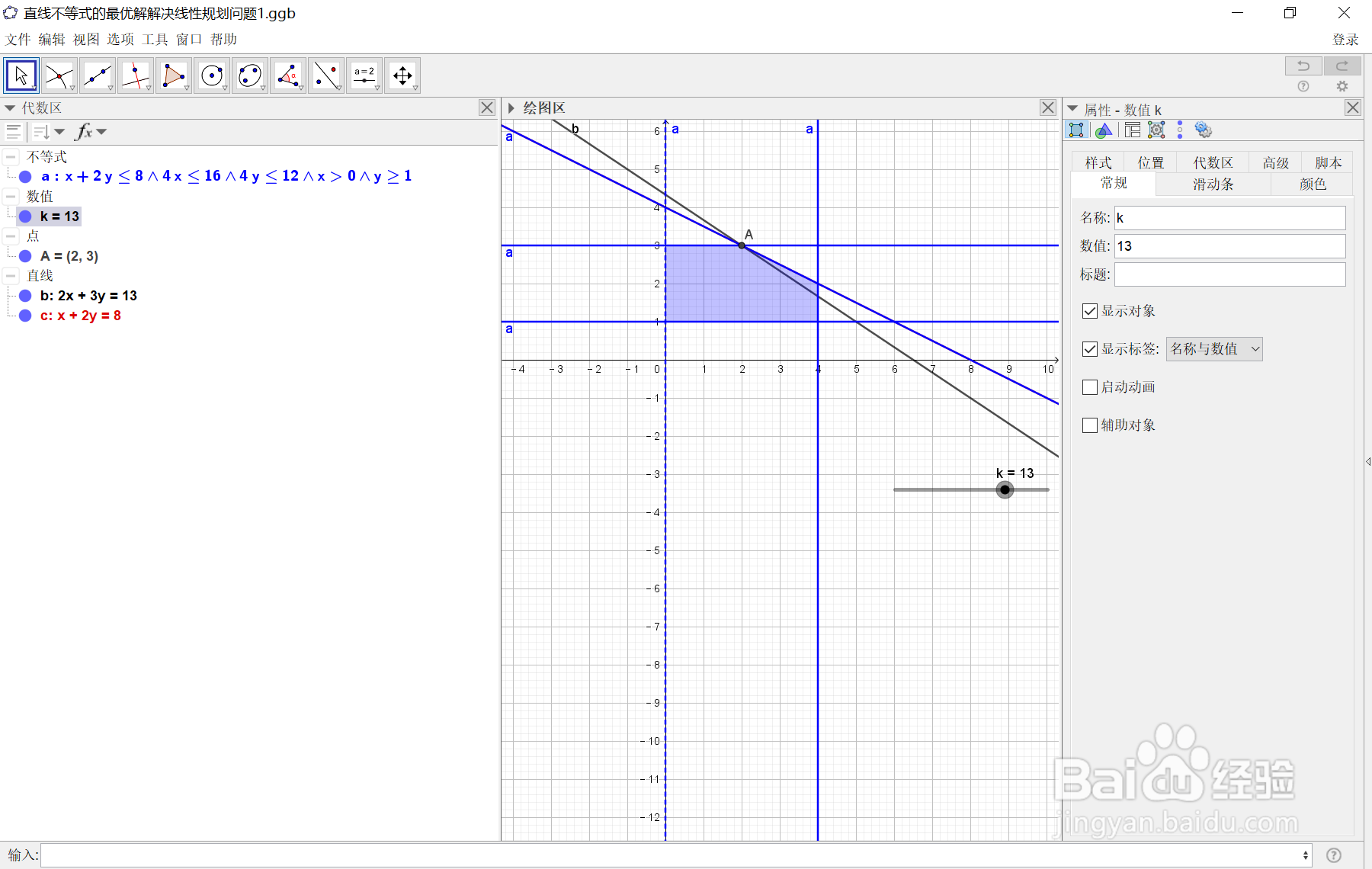
8、当k=14时,可以得到时如下图示:
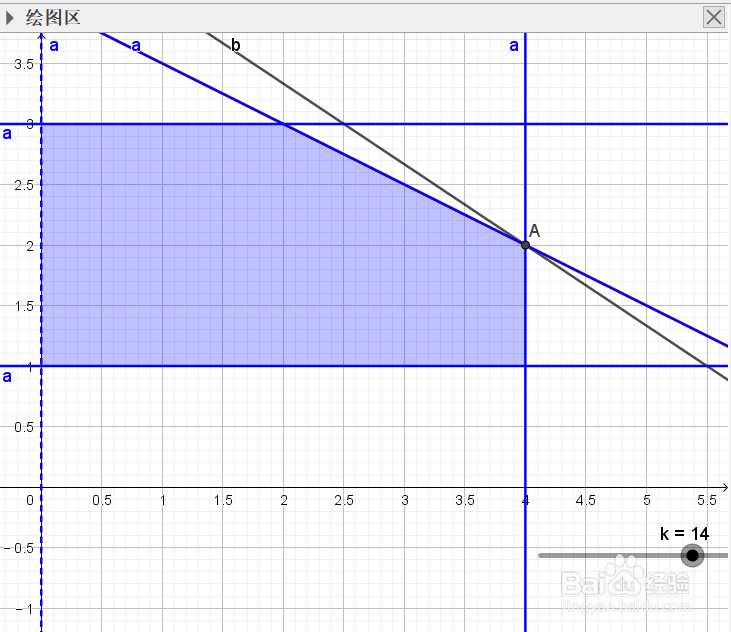

9、因此,在等值线与阴影区域的临界交汇点就是满足约束条件的最优解,该点坐标x=4,y=2,k=14,即对于目标函数max z=2x1+3x2中,x1=4,x2=2就是满足约束条件的最优解,将它们代入目标函数求得k=z=14也就是目标函数的最优值,同理!当平行线向下移动时!当它移动到刚好要离开阴影部分的临界点时!我们就能得到目标函数z的最小值,因此,图解法既可以求解最大化问题,也可以求解最小化问题.另外,由下图可以看出!线性规划的最优解出现在可行域的一个顶点上!此时线性规划问题有唯一解值。
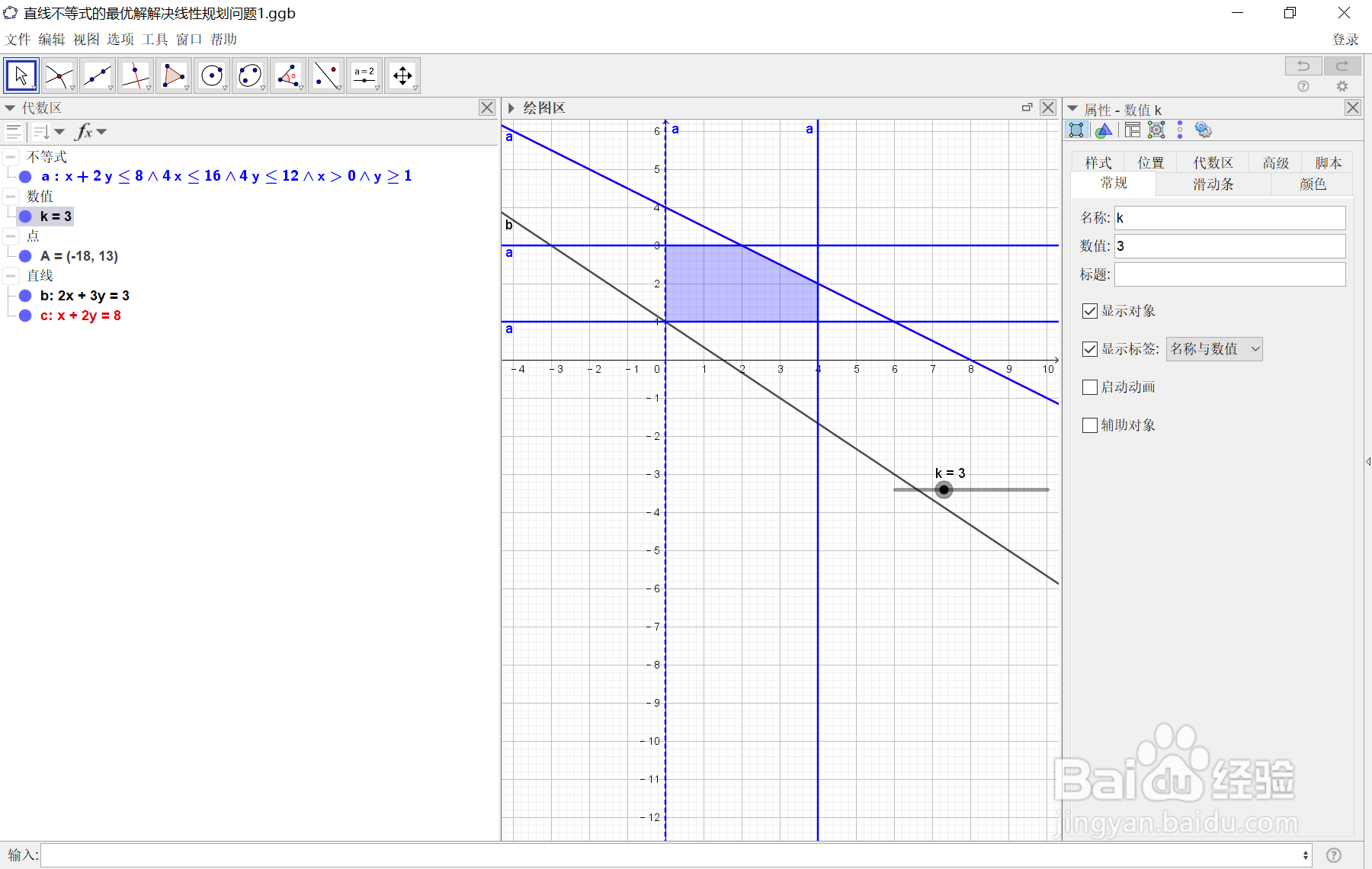
10、同理!当改变k值,直线向下移动时,当它移动到刚好要离开阴影部分的临界点时!我们就能得到目标函数z的最小值min z=2x1+3x2,此时x1=0,x2=1,z=3(最小值),因此!图解法既可以求解最大化问题,也可以求解最小化问题",如下图所示:
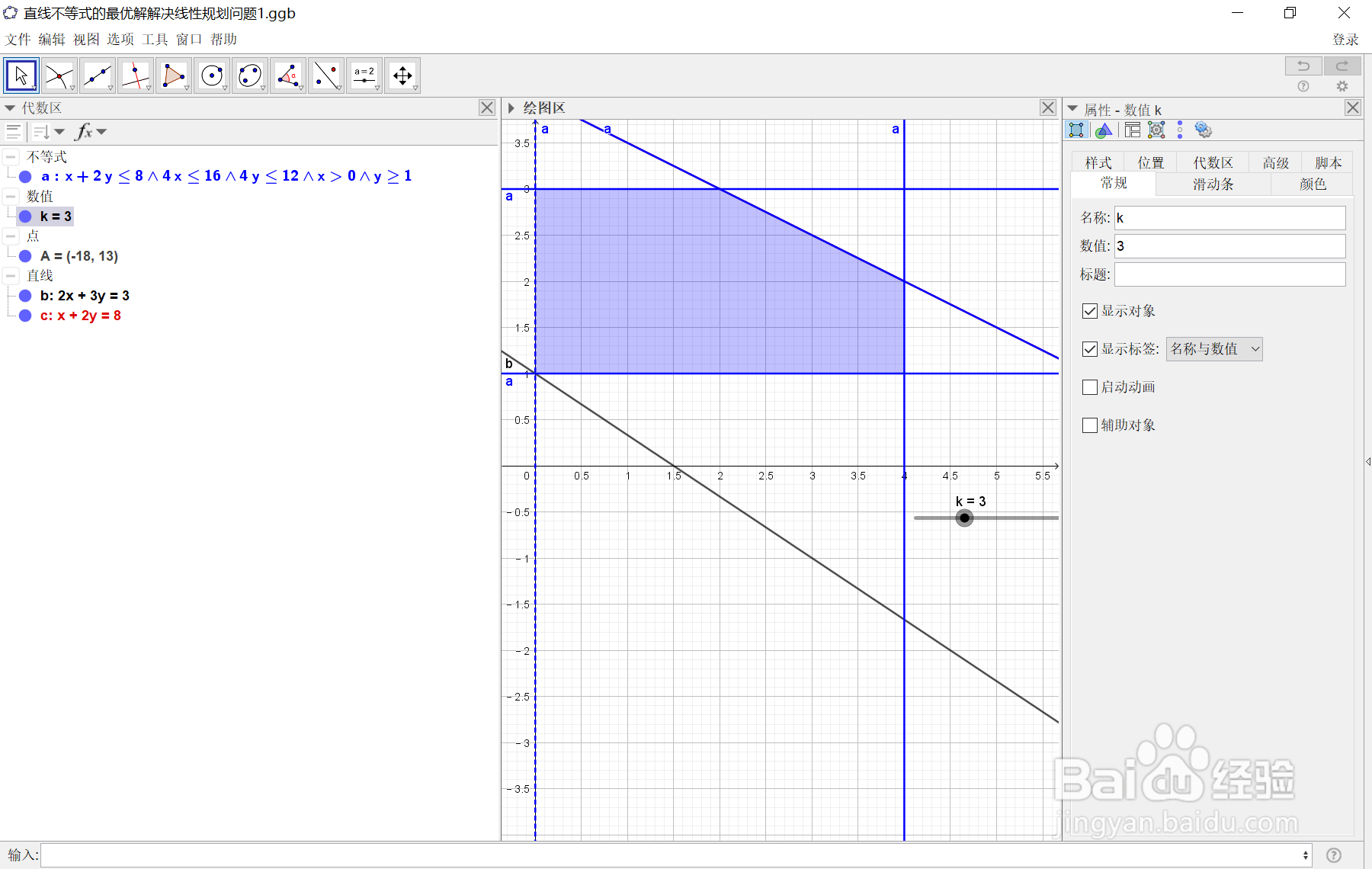
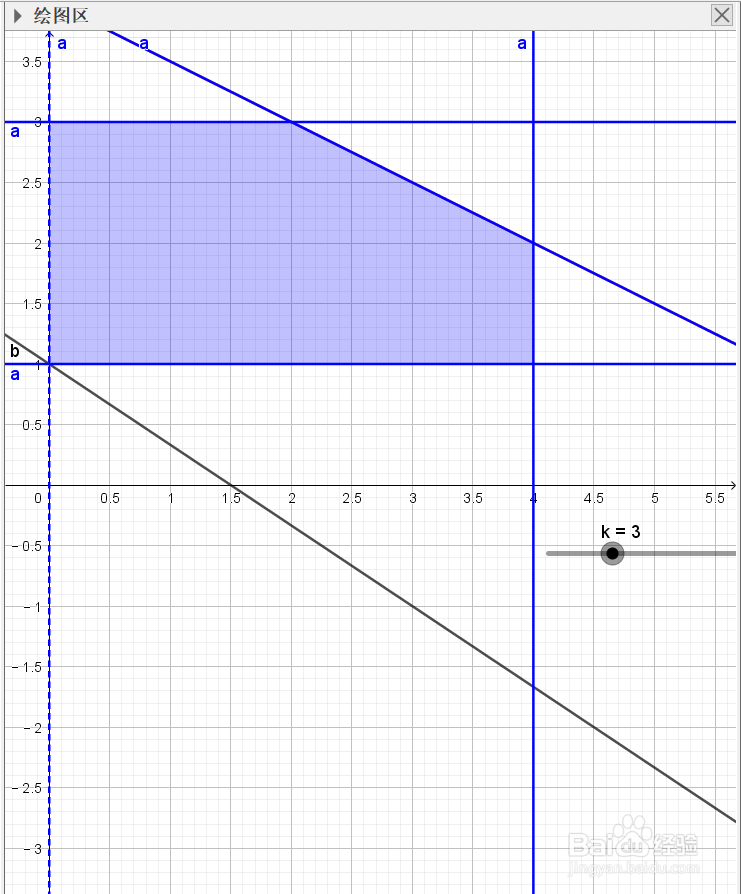
11、另外,由以上两种极大值与极小值的图可以看出:线性规划的最优解出现在可行域的一个顶点上,此时线性规划问题有唯一解,但有时线性规划问题还可能出现其他解的情况:可能有一个最优解,可能有可行解而无最优解,可能有无穷多最优解,也可能根本就没有可行解,还要看具体问题具体分析了。