二面角的正弦值怎么求

1、计算△ABD和△ADC所在平面的二面角。先给出A、B、C、D四点的坐标：{AA, BB, CC, DD} = Table[Subscript[#, n], {n, 3}] & /@ {a, b, c, d}

2、△ABD所在平面的法向量，可以用向量叉乘来表示：v1 = Cross[AA - BB, AA - DD]

3、△ADC的法向量：v2 = Cross[AA - DD, AA - CC]

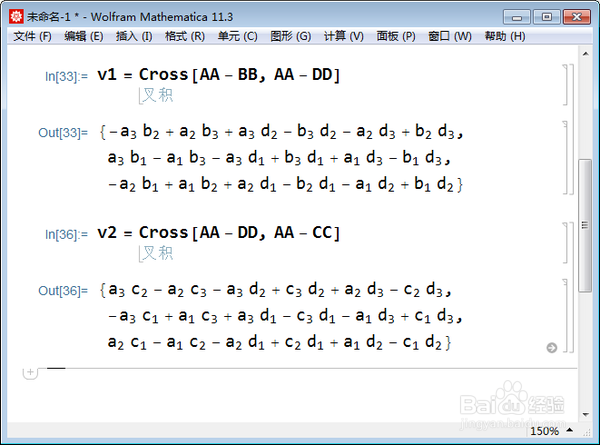
4、那么，v1和v2夹角的余弦值的平方就可以算出来：(v1.v2/(Sqrt[v1.v1]*Sqrt[v2.v2]))^2

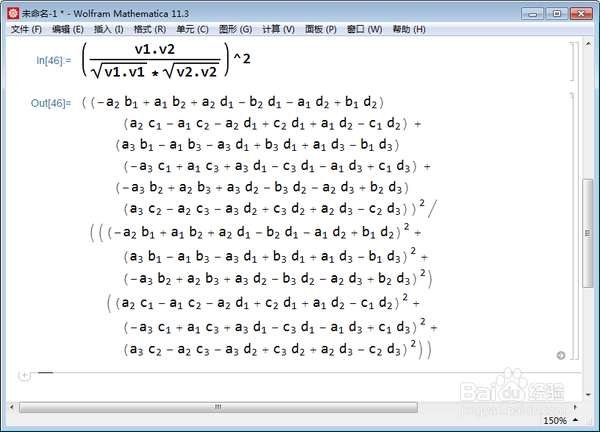
5、正弦值也就算出来了：Sqrt[1 - (v1.v2/(Sqrt[v1.v1]*Sqrt[v2.v2]))^2 // Simplify]

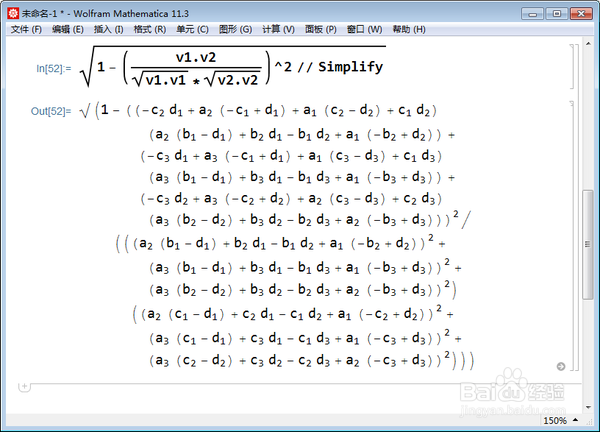
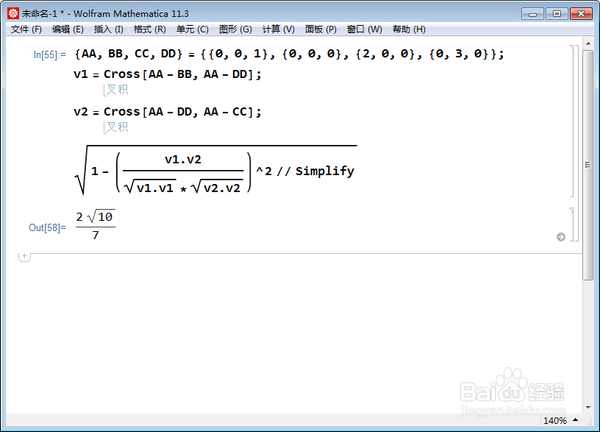
6、算一个具体的例子：{AA, BB, CC, DD} = {{0, 0, 1}, {0, 0, 0}, {2, 0, 0}, {0, 3, 0}};