用Mathematica处理多点调控曲线
1、 不了解多点调控曲线定义的人,可以参考——《多点调控曲线简介》。
先来做一个二点调控曲线,其中两个点是{0,0},{1/2,1/3},都是正调控点:
A={0,0};B={1/2,1/3};XY={x,y};
ContourPlot[1/Norm[XY - A] + 1/Norm[XY - B] == 6,
{x, -1, 1}, {y, -1, 1}, ContourStyle -> XYZColor[1, 0, 1]]
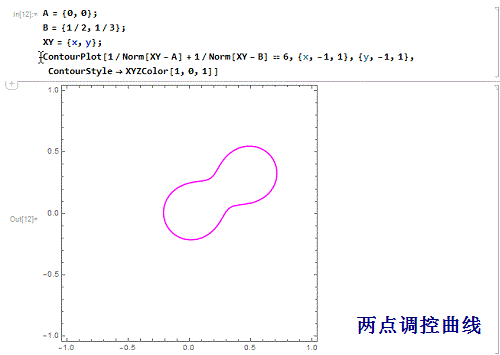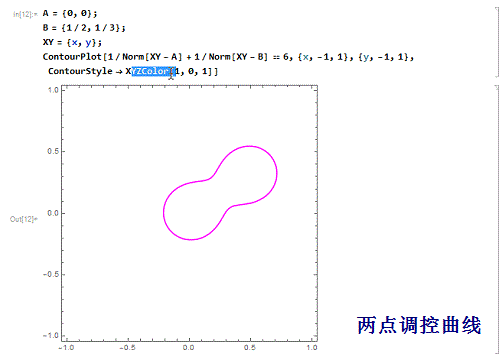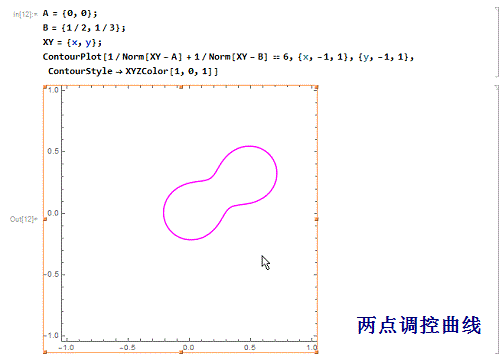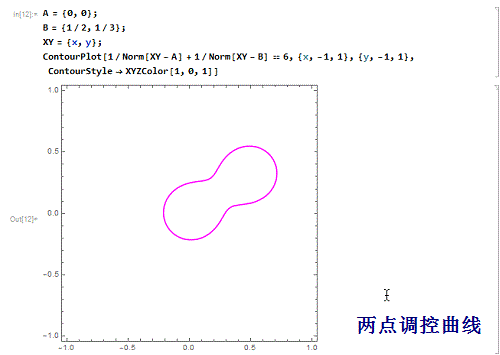
2、 我们为了看图,要把A和B也绘制出来:
Show[Graphics[{Red, Point[{A, B}]}],
ContourPlot[
1/Norm[XY - A] + 1/Norm[XY - B] == 6, {x, -1, 1}, {y, -1, 1},
ContourStyle -> XYZColor[1, 0, 1]]]

3、 把A点绘制成红色,B点绘制成绿色:
Show[Graphics[{Red, Point[A], Green, Point[B]}],
ContourPlot[
1/Norm[XY - A] + 1/Norm[XY - B] == 6, {x, -1, 1}, {y, -1, 1}]]

4、 如果点B是负调控点,会怎么样呢?
Show[Graphics[{Red, Point[A], Green, Point[B]}],
ContourPlot[
1/Norm[XY - A] - 1/Norm[XY - B] == 6, {x, -1, 1}, {y, -1, 1}]]

5、 再来两种情况的互动效果:
Manipulate[
Show[Graphics[{Red, Point[A], Green, Point[B]}],
ContourPlot[
1/Norm[XY - A] + 1/Norm[XY - B] == a, {x, -1, 1}, {y, -1, 1},
ContourStyle -> XYZColor[1, 0, 1]], ImageSize -> {500, 500}], {a,
10, 3, 0.01}]
和
Manipulate[
Show[Graphics[{Red, Point[A], Green, Point[B]}],
ContourPlot[
1/Norm[XY - A] - 1/Norm[XY - B] == a, {x, -1, 1}, {y, -1, 1},
ContourStyle -> XYZColor[1, 0, 1]], ImageSize -> {500, 500}], {a,
10, 3, 0.01}]


1、 再来看看三点调控曲线,加入一个点G:{1/3,1},如果三个点都是正调控点:
A = {0, 0}; B = {1/2, 1/3}; G = {1/3, 1}; XY = {x, y};
Show[Graphics[{Red, Point[A], Green, Point[B], Blue, Point[G]}],
ContourPlot[
1/Norm[XY - A] + 1/Norm[XY - B] + 1/Norm[XY - G] == 7,
{x, -1, 2}, {y, -1, 2}]]
图中的蓝色点,就是G。

2、 互动效果:
Manipulate[
Show[Graphics[{Red, Point[A], Green, Point[B], Blue, Point[G]}],
ContourPlot[
1/Norm[XY - A] + 1/Norm[XY - B] + 1/Norm[XY - G] == a, {x, -1,
2}, {y, -1, 2}], ImageSize -> {500, 500}], {a, 2.3, 10, 0.1}]

3、 如果把G视为负调控点,会是什么效果?
Manipulate[
Show[Graphics[{Red, Point[A], Green, Point[B], Blue, Point[G]}],
ContourPlot[
1/Norm[XY - A] + 1/Norm[XY - B] - 1/Norm[XY - G] == a, {x, -1,
2}, {y, -1, 2}], ImageSize -> {500, 500}], {a, -10, 10, 0.5}]
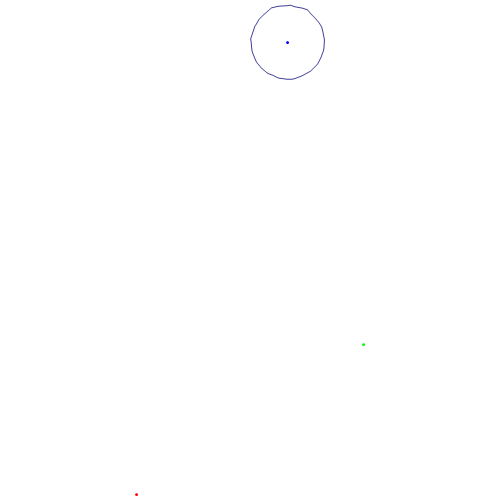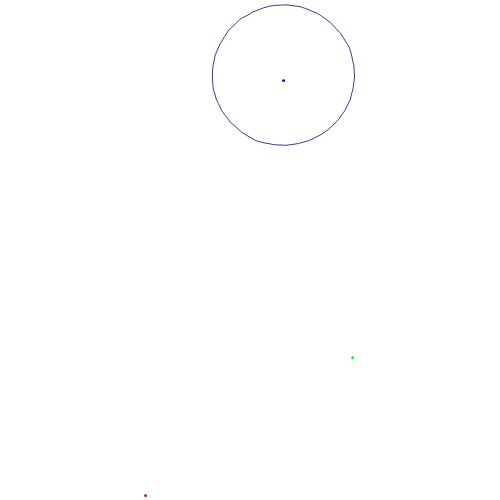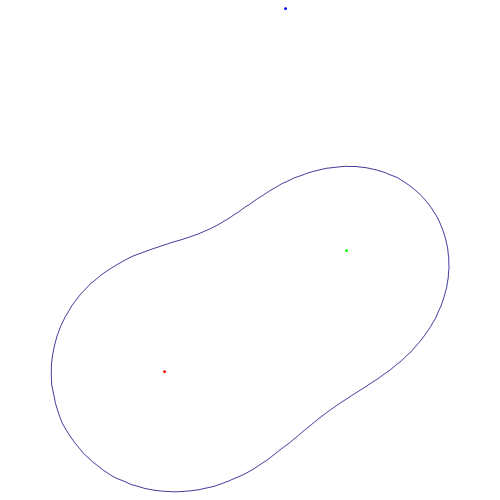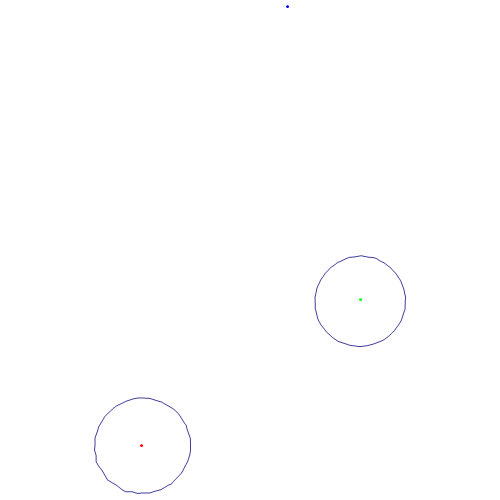
局部细化:
Manipulate[
Show[Graphics[{Red, Point[A], Green, Point[B], Blue, Point[G]}],
ContourPlot[
1/Norm[XY - A] + 1/Norm[XY - B] - 1/Norm[XY - G] == a, {x, -1,
2}, {y, -1, 2}], ImageSize -> {500, 500}], {a, -0.5, 2, 0.005}]


4、 把A、B、G变成定位器,便于移动A、B、G的相对位置(在移动的过程中,坐标也发生变化)。
Manipulate[XY = {x, y};
ContourPlot[
1/Norm[XY - A] + 1/Norm[XY - B] + 1/Norm[XY - G] == a, {x, -1,
2}, {y, -1, 2}],
{{A, {0, 0}}, Locator, Appearance -> "A"},
{{B, {1/2, 1/3}}, Locator, Appearance -> "B"},
{{G, {1/3, 1}}, Locator, Appearance -> "G"},
{a,2.3, 10, 0.1}]
和
Manipulate[XY = {x, y};
ContourPlot[
1/Norm[XY - A] + 1/Norm[XY - B] - 1/Norm[XY - G] == a, {x, -1,
2}, {y, -1, 2}], {{A, {0, 0}}, Locator,
Appearance -> "A"}, {{B, {1/2, 1/3}}, Locator,
Appearance -> "B"}, {{G, {1/3, 1}}, Locator, Appearance -> "G"}, {a,
2.3, 10, 0.1}]

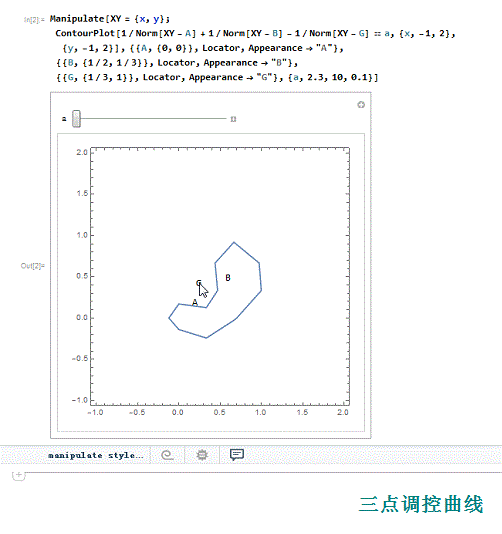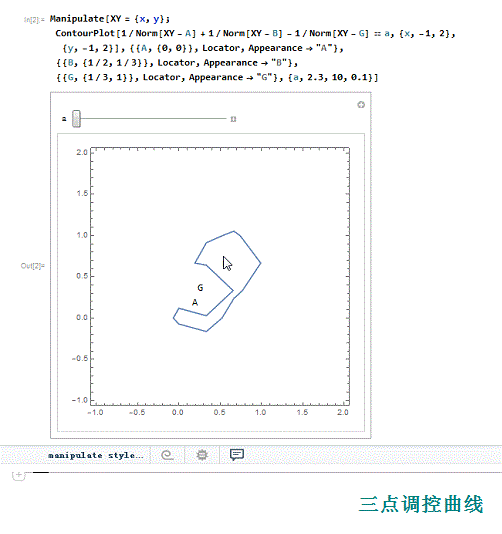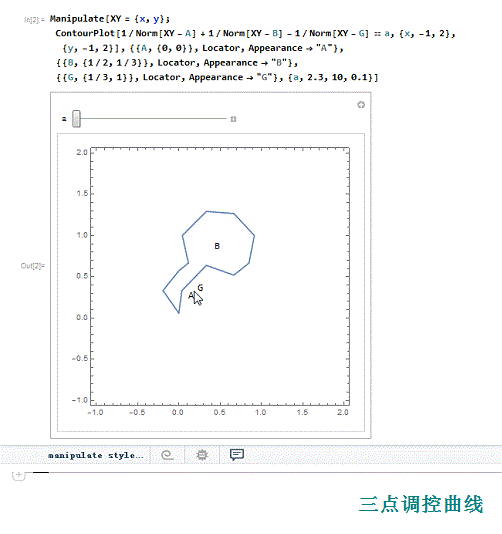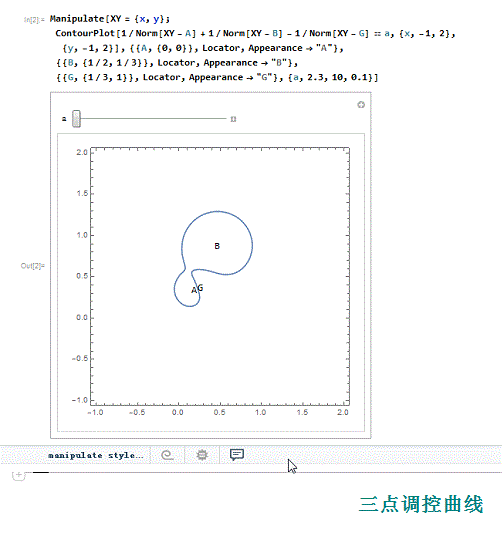
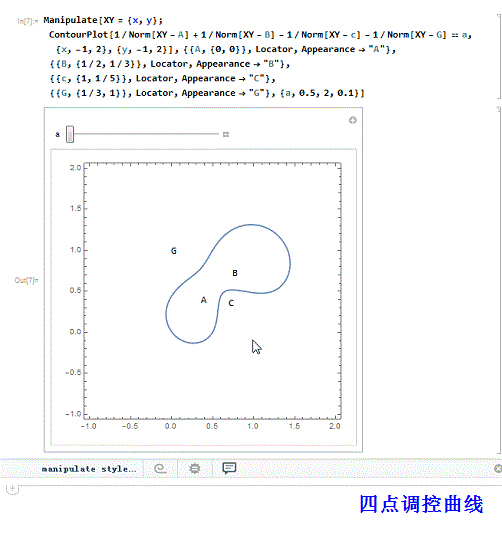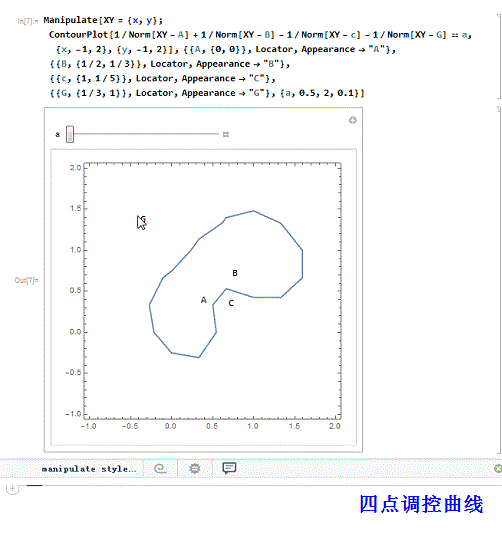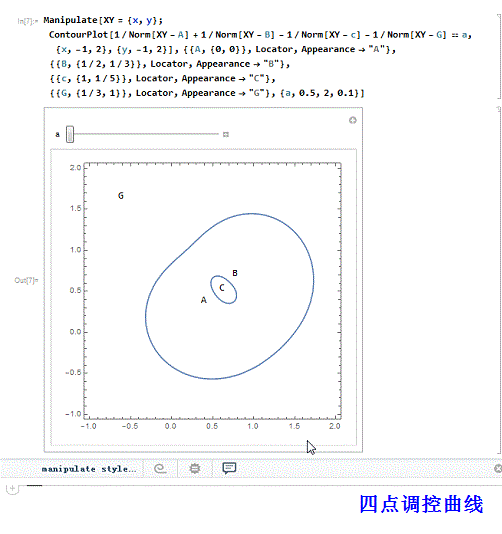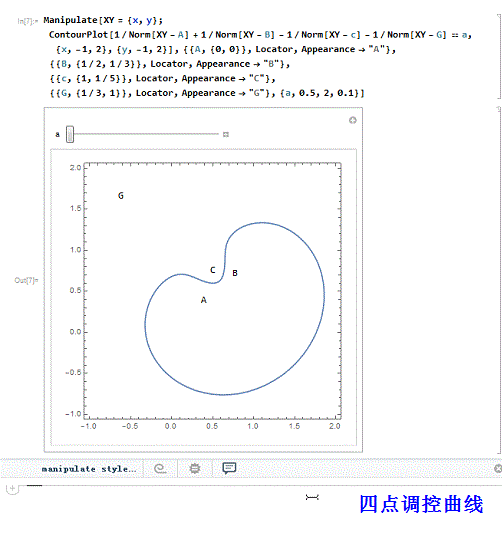
1、 我们尝试着用Mathematica的定位器来演示更多调控点的调控曲线,并试图说明,正负调控点分别位于曲线的内部和外部。
四个调控点,两正两负:
Manipulate[XY = {x, y};
ContourPlot[
1/Norm[XY - A] + 1/Norm[XY - B] - 1/Norm[XY - c] - 1/Norm[XY - G] ==a, {x, -1, 2}, {y, -1, 2}],
{{A, {0, 0}}, Locator, Appearance -> "A"},
{{B, {1/2, 1/3}}, Locator, Appearance -> "B"},
{{c, {1, 1/5}}, Locator, Appearance -> "C"},
{{G, {1/3, 1}}, Locator, Appearance -> "G"}, {a,0.5, 2, 0.1}]
2、 五个调控点,三正两负:
Manipulate[XY = {x, y};
ContourPlot[
1/Norm[XY - A] + 1/Norm[XY - B] + 1/Norm[XY - c] - 1/Norm[XY - d] -
1/Norm[XY - G] == a, {x, -1, 2}, {y, -1, 2}], {{A, {0, 0}},
Locator, Appearance -> "A"}, {{B, {1/2, 1/3}}, Locator,
Appearance -> "B"}, {{c, {1, 1/5}}, Locator,
Appearance -> "C"}, {{d, {1, 1/2}}, Locator,
Appearance -> "D"}, {{G, {1/3, 1}}, Locator, Appearance -> "G"}, {a,
1.5, 2, 0.1}]
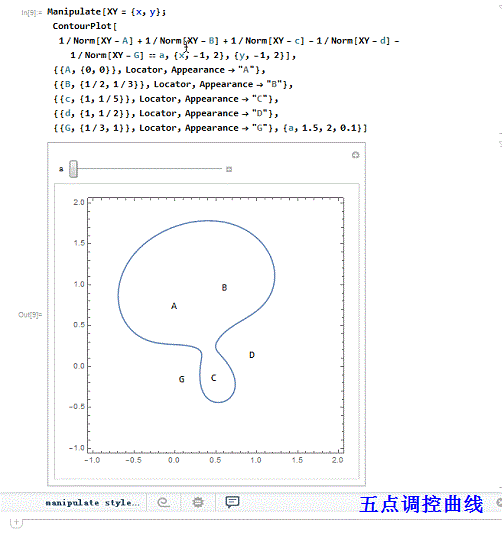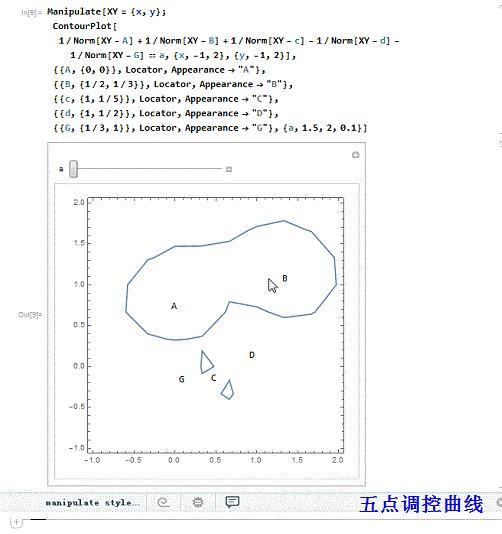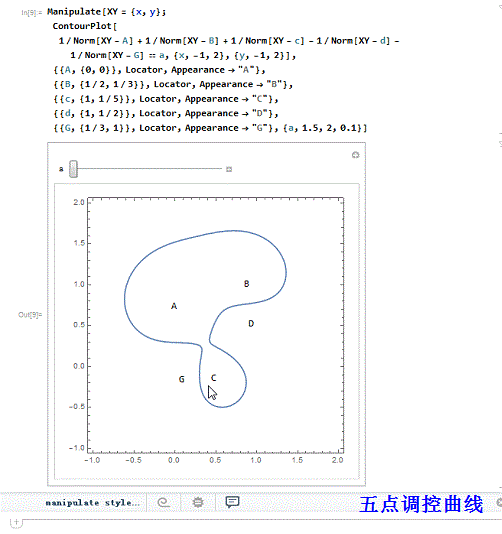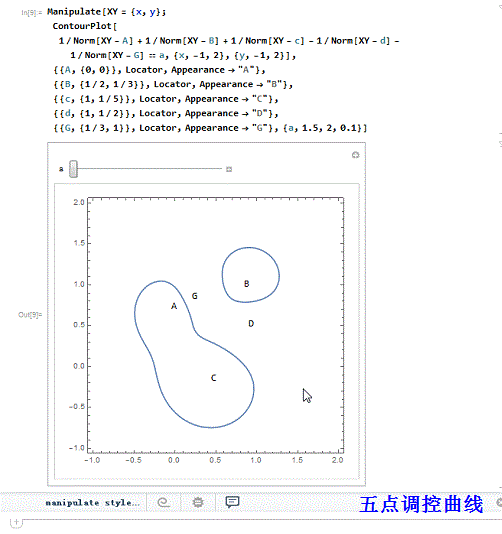
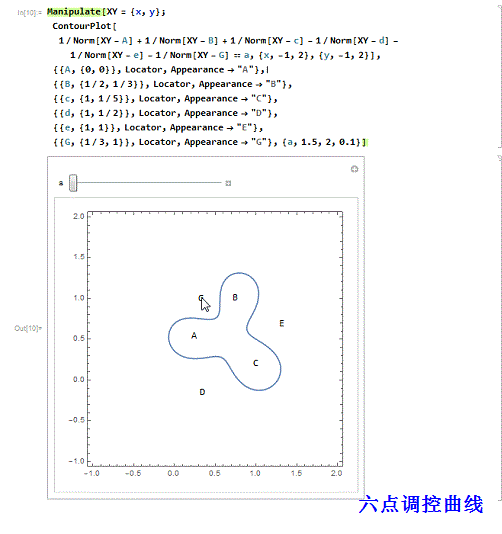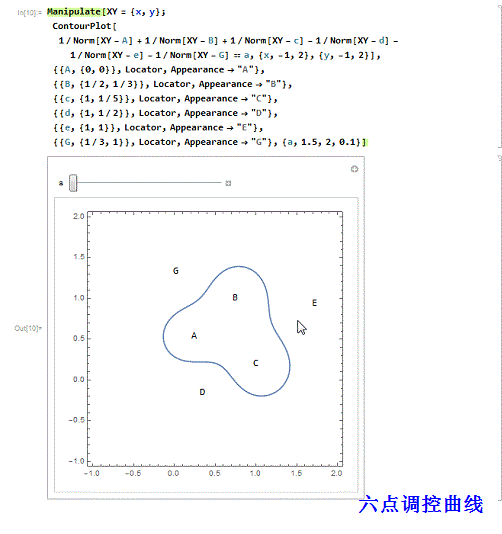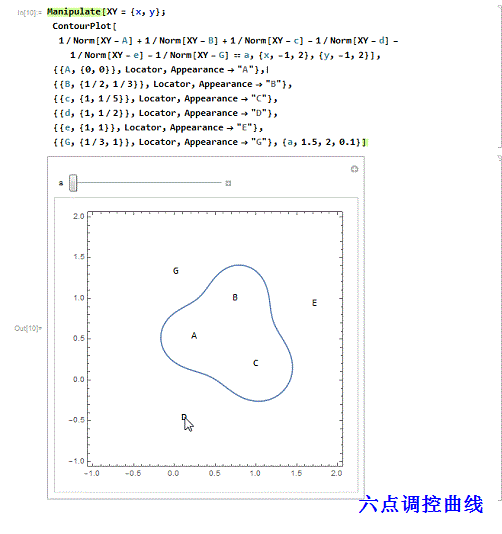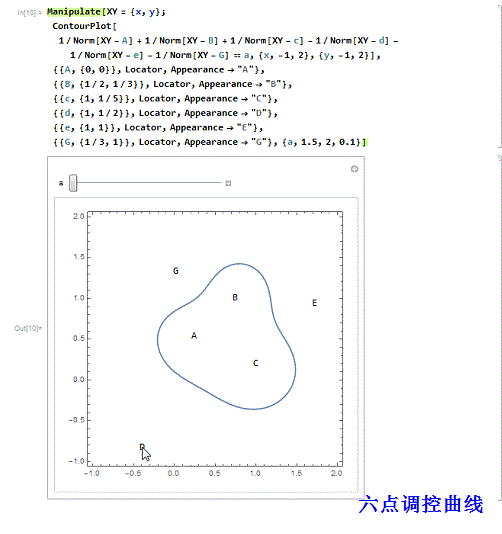
3、 三正三负的六点调控曲线:
Manipulate[XY = {x, y};
ContourPlot[
1/Norm[XY - A] + 1/Norm[XY - B] + 1/Norm[XY - c] - 1/Norm[XY - d] -
1/Norm[XY - e] - 1/Norm[XY - G] == a, {x, -1, 2}, {y, -1,
2}], {{A, {0, 0}}, Locator, Appearance -> "A"}, {{B, {1/2, 1/3}},
Locator, Appearance -> "B"}, {{c, {1, 1/5}}, Locator,
Appearance -> "C"}, {{d, {1, 1/2}}, Locator,
Appearance -> "D"}, {{e, {1, 1}}, Locator,
Appearance -> "E"}, {{G, {1/3, 1}}, Locator, Appearance -> "G"}, {a,
1.5, 2, 0.1}]