证明勾股定理,都有哪几种方式?
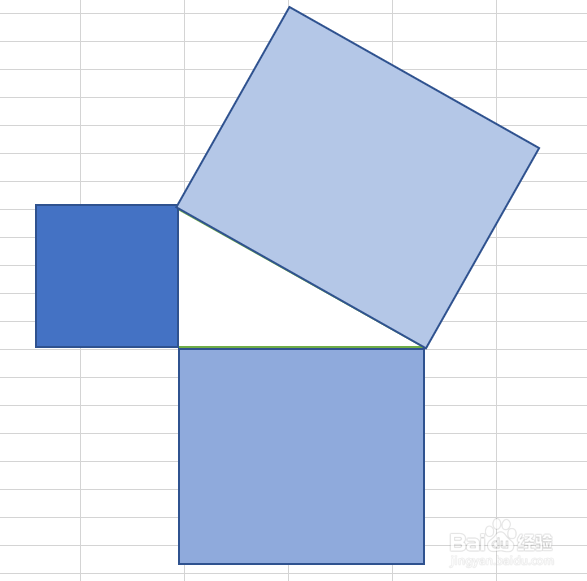
1、这是一种很常见的证明方法,具体使用的是面积来证明的。以三角形的三边分别作三个正方形,发现两个较小的正方形面积之和等于较大的那个三角形。勾股定理得到证明。
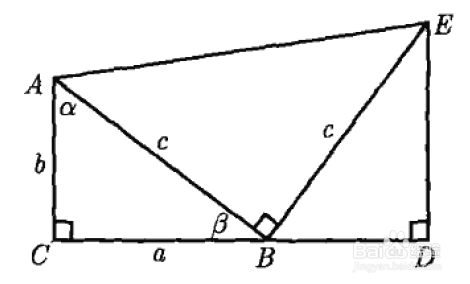
1、赵爽弦图是指用四个斜边长为c,较长直角边为a,较短直角边为c的指教三角形组成一个正方形。在这个较大的正方形里还有一个较小的正方形。通过计算整体的面积算出勾股定理。

1、梯形证明法也是一种很好的证明方法。即选两个一样的直角三角形一个横放,一个竖放,将高处的两个点相连。计算梯形的面积等于三个三角形的面积分别相加,从而证明勾股定理。
1、青出朱入图是我国古代数学家刘徽提出的一种证明勾股定理的方法,是使用割补的方法进行的。就是将两个大小不等的正方形边长分别为a,b,然后通过割补的方法将它们拼成一个较大的正方形。
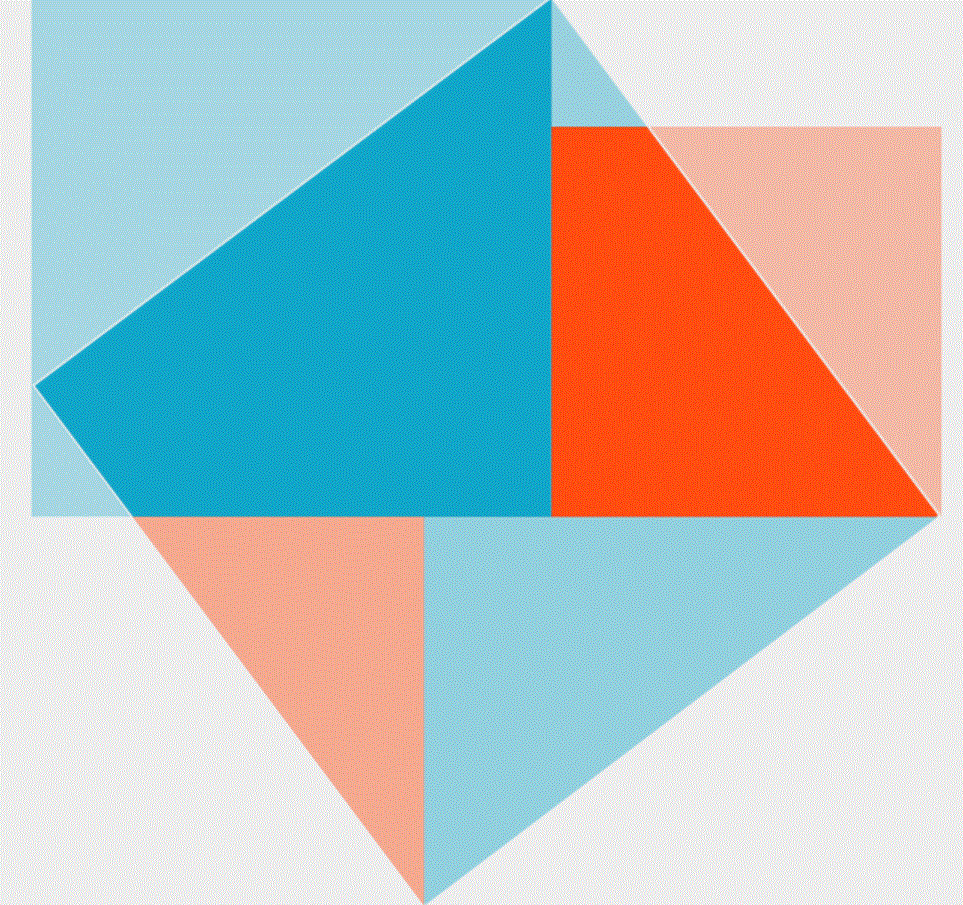
1、毕达哥拉斯的证明方法,也是证明面积相等,蛋是才去的方法是对三角形进行了移动。比如将原来的四个分散在四周的三角形,两两相组合,发现两个正方形的面积和两个长方形的面积相等。

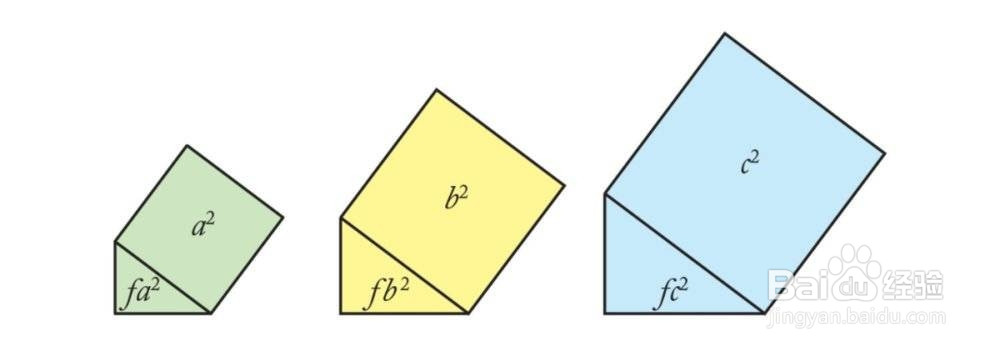
1、利用三角形的相似性来证明勾股定理。就是将三角形从直角边作垂线,这单个三角形相似。以三边分别作正方形,因为边成比例,所以面积也具有成比例的关系。

声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:63
阅读量:133
阅读量:35
阅读量:119
阅读量:161