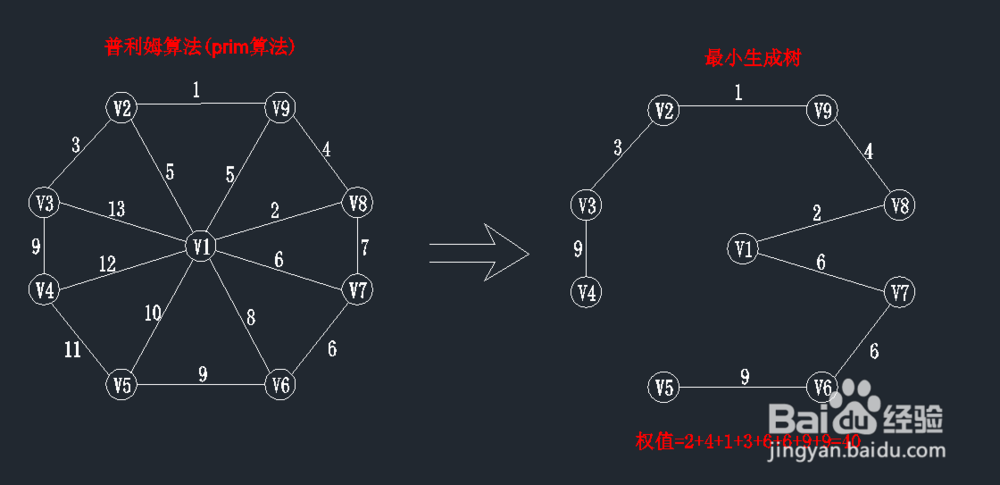
普利姆算法(prim)求最小生成树(MST)过程详解
1、最小生成树相关概念:
带权图:边赋以权值的图称为网或带权图,带权图的生成树也是带权的,生成树T各边的权值总和称为该树的权。
最小生成树(MST):权值最小的生成树。
生成树和最小生成树的应用:要连通n个城市需要n-1条边线路。可以把边上的权值解释为线路的造价。则最小生成树表示使其造价最小的生成树。
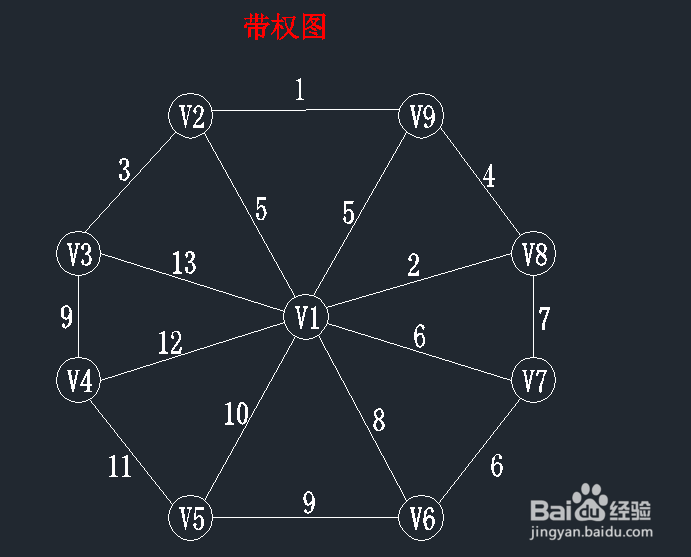
2、最小生成树的性质:
MST性质:假设G=(V,E)是一个连通网,U是顶点V的一个非空子集。若(u,v)是一条具有最小权值的边,其中u∈U,v∈V-U,则必存在一棵包含边(u,v)的最小生成树。
构造网的最小生成树必须解决下面两个问题:
(1)尽可能选取权值小的边,但不能构成回路;
(2)选取n-1条恰当的边以连通n个顶点;
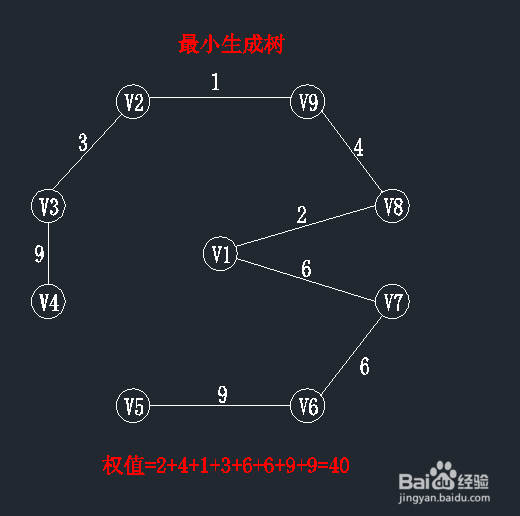
1、prim算法基本思想:
假设G=(V,E)是连通的,TE是G上最小生成树中边的集合。算法从U={u0}(u0∈V)、TE={}开始。重复执行下列操作:
在所有u∈U,v∈V-U的边(u,v)∈E中找一条权值最小的边(u0,v0)并入集合TE中,同时v0并入U,直到V=U为止。
此时,TE中必有n-1条边,T=(V,TE)为G的最小生成树。
Prim算法的核心:始终保持TE中的边集构成一棵生成树。
看了上面一大段文字是否感觉有点晕?为了便于大家更好的理解,接下来进行算法过程的分步图解!
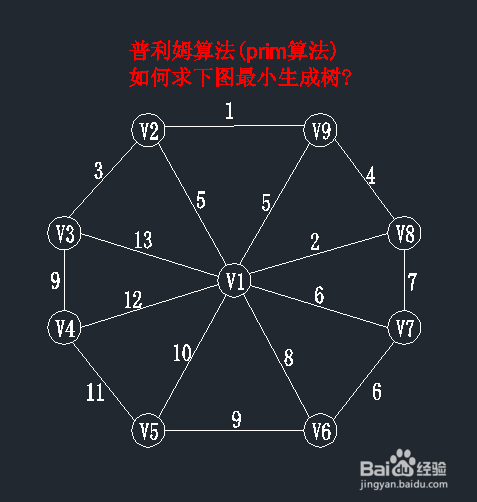
1、第一步:随意选取起点
图中有9个顶点v1-v9,集合表示为:V={v1,....,V9},每条边的边权值都在图上;在进行prim算法时,我们先随意选择一个顶点作为起始点(起始点的选取不会影响最小生成树结果),在此我们一般选择v1作为起始点,现在我们设U集合为当前所找到最小生成树里面的顶点,TE集合为所找到的边。
状态如下:U={v1}; TE={};
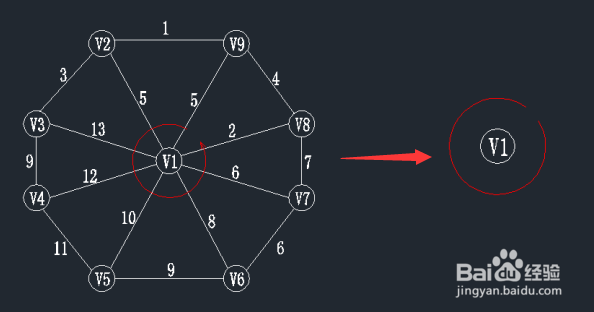
2、第二步:在前一步的基础上寻找最小权值
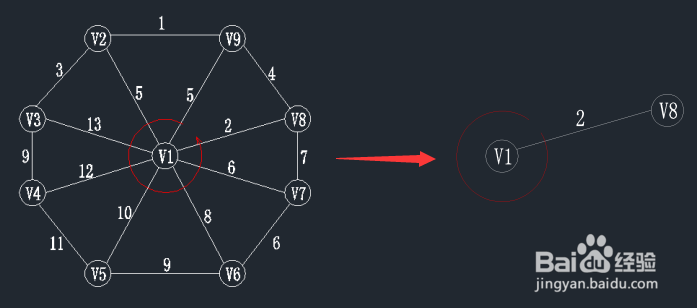
查找一个顶点在U={v1}集合中,另一个顶点在V-U集合中的最小权值,如下图,在红线相交的线上找最小值。
通过图中我们可以看到边v1-v8的权值最小为2,那么将v8加入到U集合,(v1,v8)加入到TE。
状态如下:U={v1,v8}; TE={(v1,v8)};
3、第三步:继续寻找最小权值
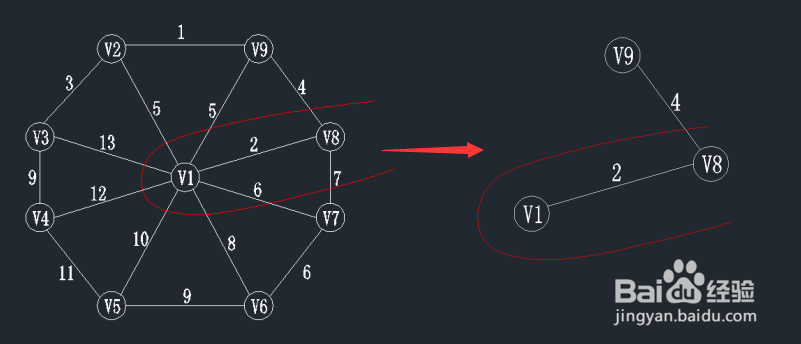
查找一个顶点在U={v1,v8}集合中,另一个顶点在V-U集合中的最小权值,如下图,在红线相交的线上找最小值。
通过图中我们可以看到边v8-v9的权值最小为4,那么将v9加入到U集合,(v8,v9)加入到TE。
状态如下:U={v1,v8,v9}; TE={(v1,v8),(v8,v9)};
4、第四步:在前一步的基础上,继续寻找最小权值
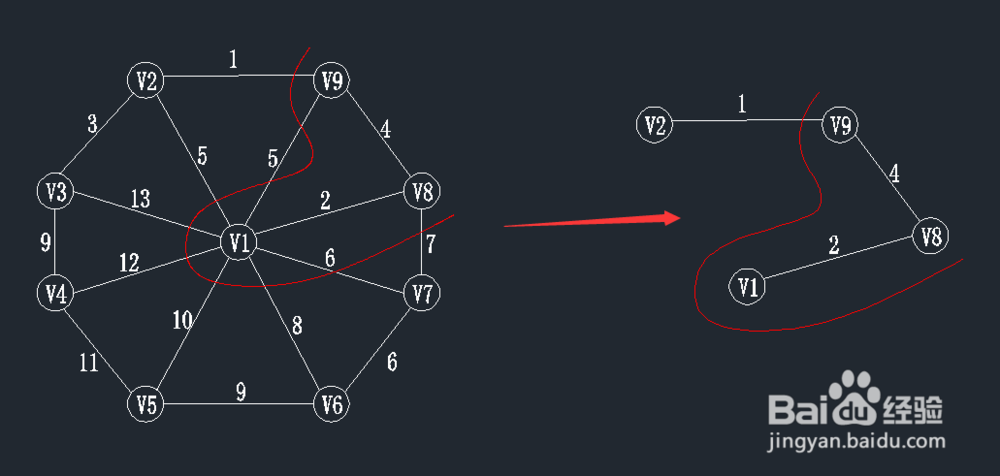
查找一个顶点在U={v1,v8,v9}集合中,另一个顶点在V-U集合中的最小权值,如下图,在红线相交的线上找最小值。
通过图中我们可以看到边v9-v2的权值最小为1,那么将v2加入到U集合,(v9,v2)加入到TE。
状态如下:U={v1,v8,v9,v2};
TE={(v1,v8),(v8,v9),(v9,v2)};
5、第五步:继续在前一步的基础上,寻找最小权值
查找一个顶点在U={v1,v8,v9,v2}集合中,另一个顶点在V-U集合中的最小权值,如下图,在红线相交的线上找最小值。
通过图中我们可以看到边v2-v3的权值最小为3,那么将v3加入到U集合,(v2,v3)加入到TE。
状态如下:U={v1,v8,v9,v2,v3};
TE={(v1,v8),(v8,v9),(v9,v2),(v2,v3)};

6、第五~九步:继续在前一步的基础上,寻找最小权值
如此循环一下直到找到所有顶点为止。到这大家应该对普利姆算法求解最小生成树的过程有所知晓,但需注意以下三点:
(1)每次都选取权值最小的边,但不能构成回路,构成环路的边则舍弃。如图中的(v1,v9),(v1,v2)等构成回路舍弃
(2)遇到权值相等,又均不构成回路的边,随意选择哪一条,均不影响生成树结果。如图中的(v3,v4),(v6,v5)权值均为9,选择哪一条在先均不影响最小生成树的生成结果。
(3)选取n-1条恰当的边以连通n个顶点。
完整的算法步骤如图所示:

1、(1)最小生成树(MST)是指权值最小的生成树。
(2)prim算法是求最小生成树的算法之一,其他算法还有kruskal算法
(3)其时间复杂度为O(n^2),与边得数目无关。prim算法适合稠密图。