如何利用Lingo进行非线性规划

1、卡隆公司的新肥料

问题 卡隆（Carron）化学公司的年轻工程师R 和D 合成了一种轰动一时的新肥料，只用两种基本原料来制造. 公司想利用这个机会生产尽可能多的这种新肥料，公司目前有资金40000美元，可购买单价分别为8000美元的原料A和5000美元的原料B. 当用数量为x1和x2两种原料合成时，肥料的数量Q 由下式给出：

Q =4x1+2x2-0.5x1^2 -0.25x2 ^2

试确定购买原料的计划.

问题分析 计划的目标是用有限的钱购买的原料，生产出最多的新肥料. 肥料的数量与原料数量不是线性关系. 因此这个优化问题是一个非线性规划问题.

模型建立

决策变量：显然是原料A, B的数量x1和x2 .

目标函数：问题中已经给出，即

Q =4x1+2x2-0.5x1^2 -0.25x2 ^2

约束条件：

资金约束 即购买原料的总费用不能超过公司现有资金40000 美元；

非负约束 购买两种原料的数量都是非负数.

综上可得数学模型如下：

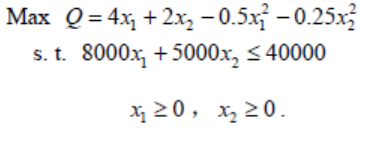
2、模型求解

非线性规划也可以用LINGO 求解. 在LINGO11新建文档中输入如下代码：

model:

init:

x1=0.0;

x2=0.0;

endinit

max=4*x1+2*x2-0.5*x1^2-0.25*x2^2;

8000*x1+5000*x2<=40000;

x1>=0;

x2>=0;

end

得到输出结果如下：

3、结果分析 由于非线性规划目标函数不一定是线性函数，可行域也不一定是多边形区域，所以最优解很难得到. 现有的理论和算法都不能保证得到整个可行域上的最优解，即全局最优解（Global optimal solution）. 只能得到在可行域某个局部的最优解，称为局部最优解（Local optimal solution）. LINGO 求解非线性规划也不能保证得到全局最优解. 决策变量初值的不同设定值，可能导致最后的结果不同. 本例模型简单，不同的初值得到的都是同样的最优解x1 =3.157906和x2= 2.947305