椭圆二级结论是什么呢

1、当平面与二次锥面的母线平行，且不过圆锥顶点，结果为抛物线。

2、当平面与二次锥面的母线平行，且过圆锥顶点，结果退化为一条直线。

3、当平面只与二次锥面一侧相交，且不过圆锥顶点，结果为椭圆。

4、当平面只与二次锥面一侧相交，且不过圆锥顶点，并与圆锥的对称轴垂直，结果为圆。

5、当平面与二次锥面两侧都相交，且不过圆锥顶点，结果为双曲线（每一支为此二次锥面中的一个圆锥面与平面的交线）。

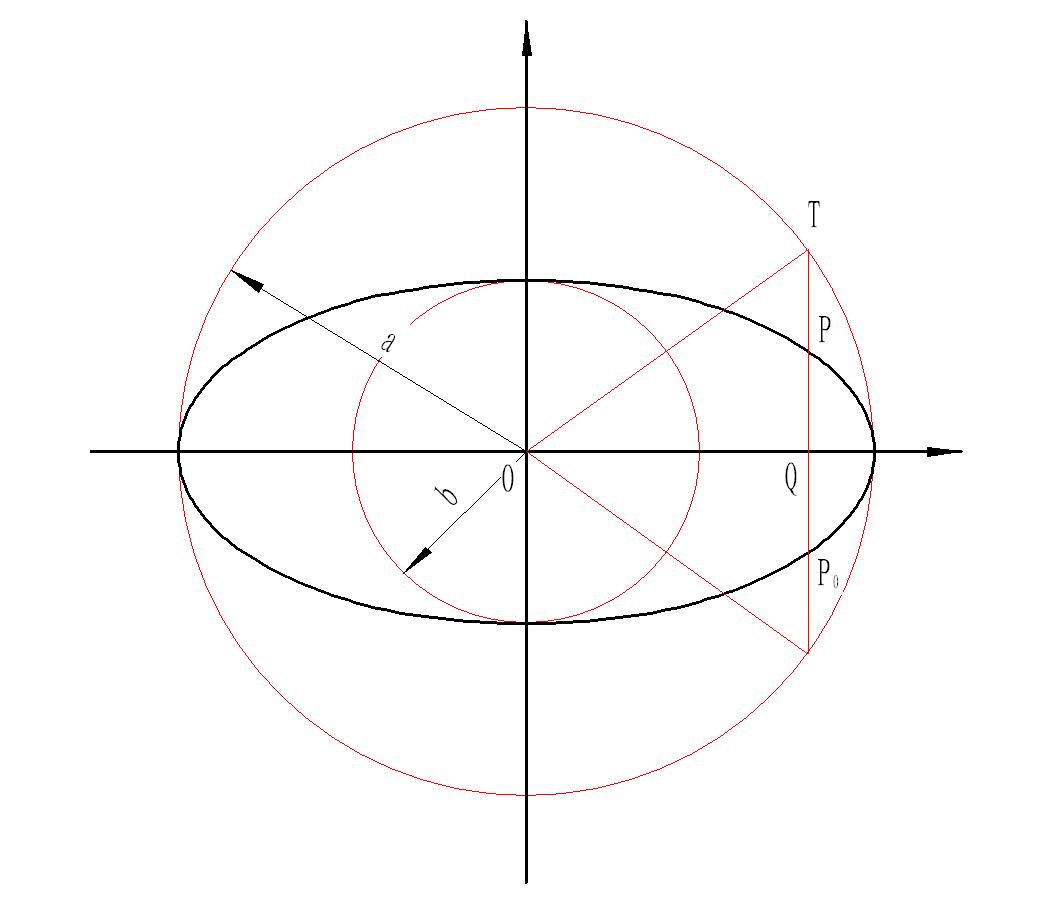
第一定义：平面内与两定点F1、F2的距离的和等于常数2a（2a≥｜F1F2｜）的动点P的轨迹叫做椭圆。即：其中两定点F1、F2叫做椭圆的焦点，两焦点的距离｜F1F2｜=2c≤2a叫做椭圆的焦距。P为椭圆的动点。

第二定义：椭圆平面内到定点F（c，0）的距离和到定直线l：x=a/c（F不在l上）的距离之比为常数从C/A,（即离心率，0<e<1）的点的轨迹是椭圆。