因式分解四种基本方法

1、公式法。

常用的公式包括：

平方差公式，立方差和立方和公式，完全平方公式。

比如，x^4-y^4，可以套用平方差公式：

x^4-y^4=(x^2+y^2)(x^2-y^2)

注意，x^2-y^2可以继续套用平方差公式。

2、提取公因式法：

(a-b)(m+1)-(b-a)(n-1)

前后两项都含有因式a-b，可以提取出来：

(a-b)(m+1)-(b-a)(n-1)

=（a-b）（m+1+n-1）

=（a-b）（m+n）

3、分组分解法：

9ax^2+9bx^2-a-b

前两项含有公因式9x^2，可以先分解：

9ax^2+9bx^2-a-b=9x^2(a+b)-a-b

然后再提取公因式a+b：

9x^2(a+b)-a-b=（a+b）（9x^2-1）

注意，9x^2-1可以继续套用平方差公式。

4、十字相乘法：

6x^2+22x+20

x^2的系数可以分解为2*3，2可以分解为4*5，而2*5+3*4=22，所以分解为：

6x^2+22x+20=（2x+4）（3x+5）

注意，2x+4还有公因式2。

5、Mathematica可以使用Factor实现因式分解：

Factor[6 x^2 + 22 x + 20]

6、一些特别复杂的多项式，也可以分解：

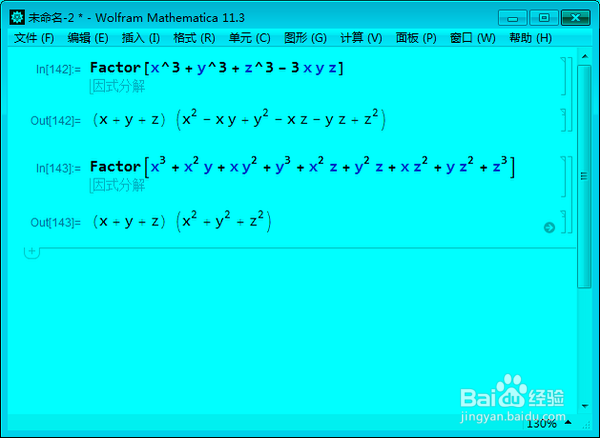
Factor[x^3 + y^3 + z^3 - 3 x y z]

Factor[x^3 + x^2 y + x y^2+y^3 + x^2 z + y^2 z+x z^2+y z^2+z^3]