ufunc的方法——python.numpy基础

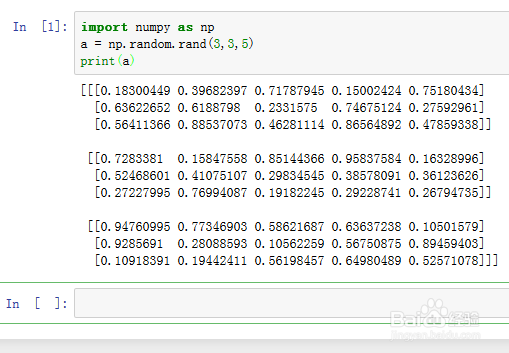
1、先构造一个三维数组：

import numpy as npa = np.random.rand(3,3,5)

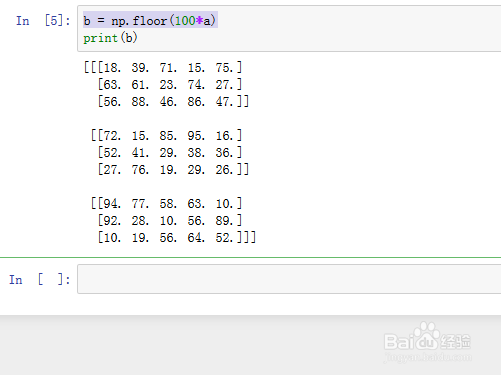
2、np.floor是一个ufunc函数，它是一个一元函数——取整函数，可以做用于a里面的每一个数字，且保持数组结构不变，仍旧是三维的3*3*5的数组：

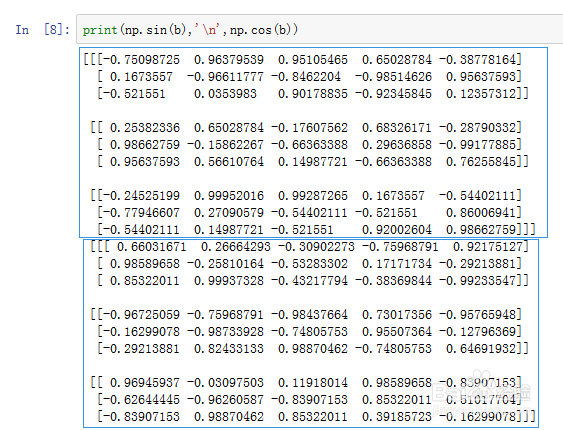
3、类似的一元ufunc函数还有很多，比如所有的初等数学函数：

print(np.sin(b),'\n',np.cos(b))

4、np.add是一个多元的ufunc函数：

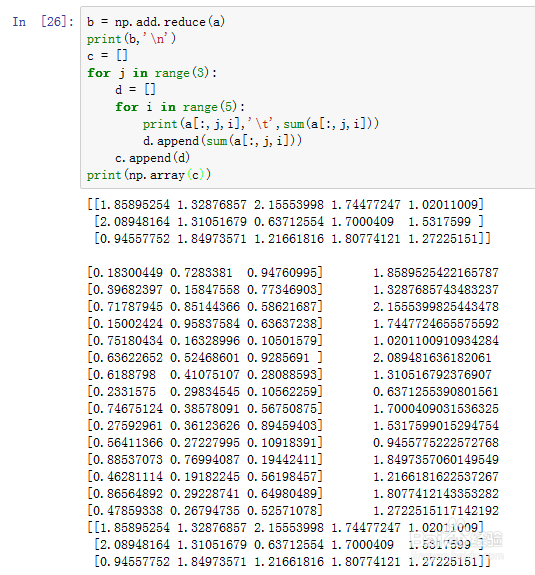
b = np.add.reduce(a)

这里，reduce的作用，是把add函数作用于数组a的第一层每一个子数组，计算这些元素的和。

具体的作用结果是：

c = []for j in range(3):    d = []    for i in range(5):        #print(a[:,j,i],'\t',sum(a[:,j,i]))        d.append(sum(a[:,j,i]))    c.append(d)print(np.array(c))

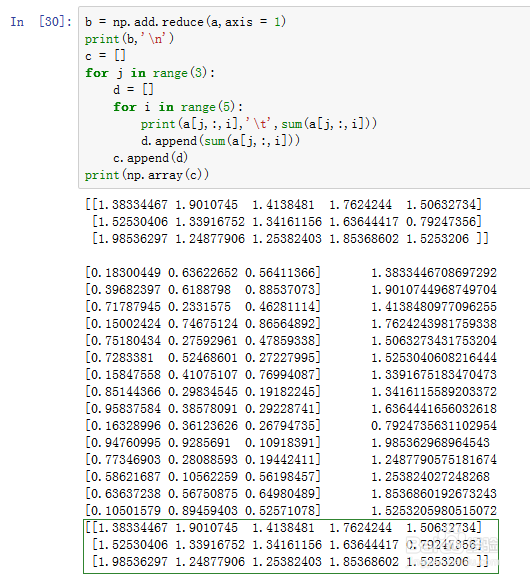
5、b = np.add.reduce(a,axis = 1)

这里指定了add作用于a的第二层子数组，具体如下：

c = []for j in range(3):    d = []    for i in range(5):        #print(a[j,:,i],'\t',sum(a[j,:,i]))        d.append(sum(a[j,:,i]))    c.append(d)print(np.array(c))

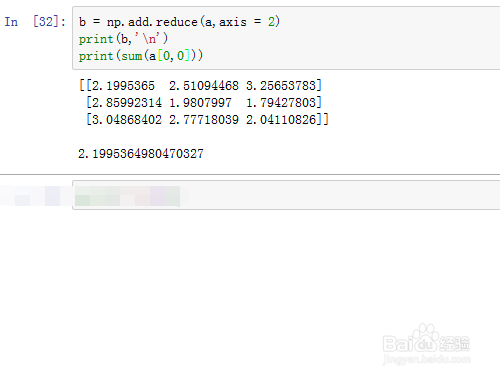
6、b = np.add.reduce(a,axis = 2)

将add函数作用于a的第三层子数组：

print(sum(a[0,0]))

7、给出一个一维数组：

import numpy as npa = np.floor(np.random.rand(6)*10)

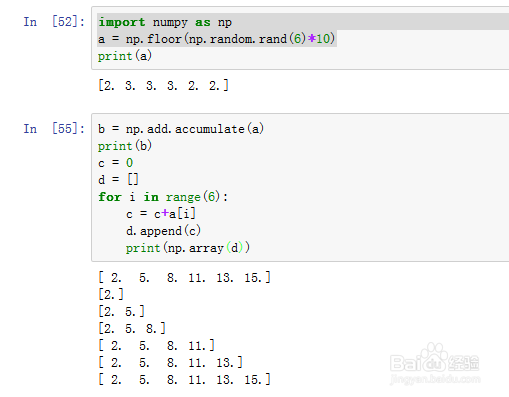
从左往右累计a里面的元素之和：

b = np.add.accumulate(a)

具体的类似于：

c = 0d = []for i in range(6):    c = c+a[i]    d.append(c)    print(np.array(d))

8、给出一维数组a：

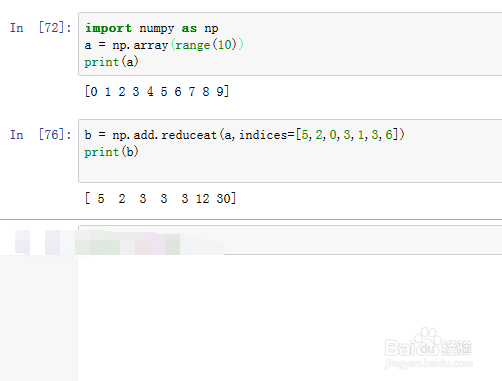
import numpy as npa = np.array(range(10))

看看下面的函数：

b = np.add.reduceat(a,indices=[5,2,0,3,1,3,6])

9、reduceat的作用比较特殊——————

如果indices的第i个元素不是最后一个元素：

       如果indices的第i个元素比后一个元素（第i+1个元素）小，那么计算

              np.add(a[indices[i]:indices[i+1]])

              并把计算结果返回给b[i]；

       否则，把a[indices[i]]返回给b[i]；

反之，indices的第i个元素是最后一个元素：

        把a[indices[i]:]返回给b[i]。

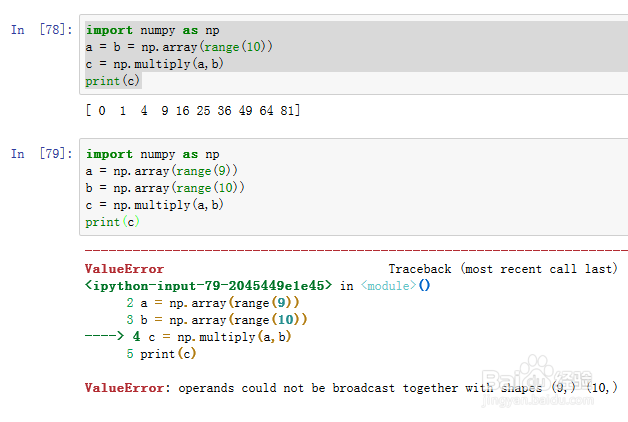
10、import numpy as npa = b = np.array(range(10))c = np.multiply(a,b)

multiply把a和b的对应元素相乘，得到一个与a和b的结构相同的新数组;

所以，a和b的结构必须一样；

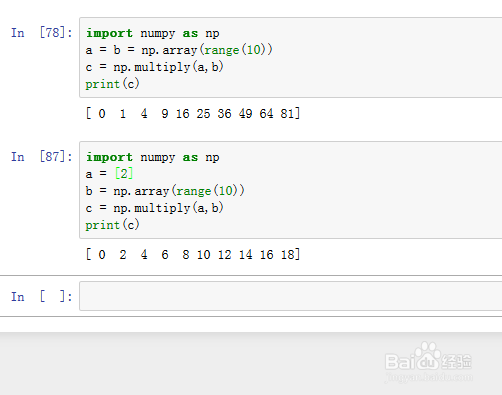
注意，当a或b的某一个数组只有一个元素，在multiply里面，会自动补全为与另一方相同结构的数组。

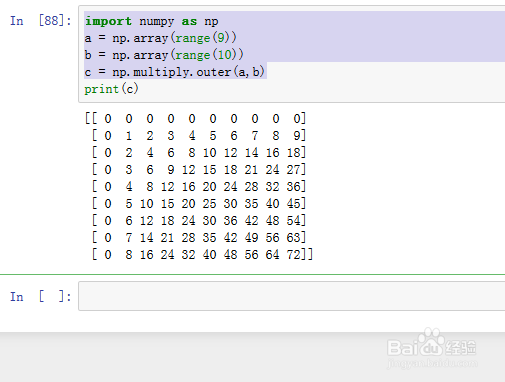
11、import numpy as npa = np.array(range(9))b = np.array(range(10))c = np.multiply.outer(a,b)

c是a和b里面的元素的乘法表；

这里a和b的结构不必完全相同，比较自由。

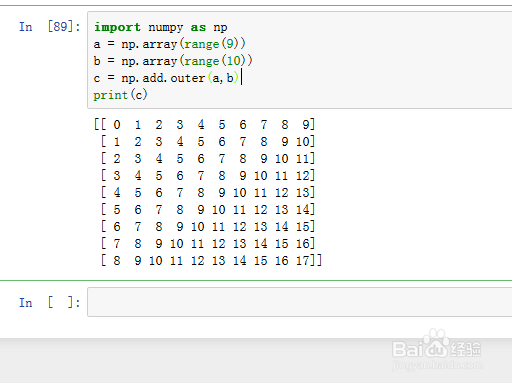
12、加法表：

import numpy as npa = np.array(range(9))b = np.array(range(10))c = np.add.outer(a,b)

幂方表：

import numpy as npa = np.array(range(6))b = np.array(range(5))c = np.power.outer(a,b)

其中，a里面的元素是底数，b里面的元素是指数。