行测备考：妙用极限思想 巧解和定最值问题

国考行测中数量关系部分是很多同学心中的痛，不仅是因为解题难度大，更是因为很多题目判断不清题型特征，无从下手。对于能在短时间分清类型的题目，建议大家认真分析，遵循解题方法求解不要放弃，其中和定最值问题就属于这类题型。

方法/步骤

 一、题型特征 

题目中若干个量和为定值，问题让求某个量的最大值或者最小值。

【例1】

假设7个相异正整数的和是98，已知这7个数中第三大的数为18，则此7个正整数中最大的数最大是多少?

【题干分析】题目问题让求最大的量的最大值，判断题型为极值问题，题干中提到“假设7个相异正整数的和是98”，告诉我们7个量和为定值，故而判断此题为和定极值问题。

【例2】

8名工人在流水线工作，平均每人一个小时完成23个零件。已知每名工人的工作效率互不相同，且效率最快的工人一小时完成了27个零件，则效率最慢的工人一小时最少完成多少个零件?

【题干分析】题目问题让求最慢的工人最少完成多少零件，判断题型为极值问题，题干中提到“8名工人在流水线工作，平均每人一个小时完成23个零件”，已知8个人的平均量，变相的告知8个人每小时共计完成184个零件，和为定值，故而判断此题为和定极值问题。

二、解题原则 

若干个量和一定时，求某个量的最大值，原则是让剩余量尽可能小;

若干个量和一定时，求某个量的最小值，原则是让剩余量尽可能大。

【例1】

假设7个相异正整数的和是98，已知这7个数中第三大的数为18，则此7个正整数中最大的数最大是多少?

A.47 B.51 C.53 D.57

【答案】B

【解析】7个数和一定，要求最大数的最大值，原则为其余量尽可能小。

 7个数从大到小依次排序为

x+19+18+4+3+2+1=98 解得x=51，答案为B。

【例2】8名工人在流水线工作，平均每人一个小时完成23个零件。已知每名工人的工作效率互不相同，且效率最快的工人一小时完成了27个零件，则效率最慢的工人一小时最少完成多少个零件?

A.16 B.17 C.20 D.21

【答案】A

【解析】8个人每小时完成零件数总和为184个，要求最慢的工人一小时最少完成多少个零件，原则为让其余人每小时完成零件数尽可能大。每名工人的工作效率互不相同，则从多到少依次排序为：

27+26+25+24+23+22+21+x=184 解得x=16，答案为A。

二、拔高训练 

(一)当题干中给出的不是总和，而是若干量的平均数时，可以结合盈余亏补的思想快速解题。

【例】

8名工人在流水线工作，平均每人一个小时完成23个零件。已知每名工人的工作效率互不相同，且效率最快的工人一小时完成了27个零件，则效率最慢的工人一小时最少完成多少个零件?

A.16 B.17 C.20 D.21

【解析】题型判定为和定最值问题，题干中出现8个人每小时完成的平均个数，要求最慢的工人一小时最少完成多少个零件，原则为让其余人每小时完成零件数尽可能大，结合盈余亏补求解

第一、二、三、四、五名比8个人的平均效率分别多4、3、2、1、0个，第六、七名8个人的平均效率分别少1、2个，综合来看，前七名比8个人的平均数多7个，则第八名应该比平均数少7个，即23-7=16个。

(二)当题干中出现和一定时，要求最大量的最小值(或最小量的最大值)时，原则为让所有的量尽可能平均。

【例】

6名同学参加一次百分制考试，已知6人的分数是互不相同的整数。若6名同学的总分是513分，求分数最低的最多得了多少分?

【答案】83

【解析】6个人总和为513，要求最小量的最大值，方法为其余量尽可能小。

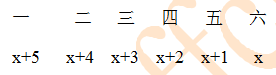
6个人构成等差数列，则第三、四名的中间值为513÷6=85……3，第三名为86，第四名为87。

可知第六名最多为83分。

综合来看，和定最值问题题型易于判断，方法易于掌握，各位考生适当进行相应题目训练就可以掌握吸收，考场上遇到该题型不要轻易放弃。