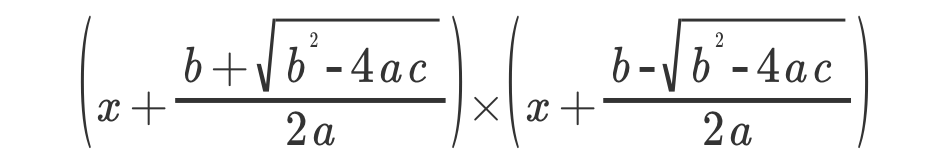如何用Slide and divide因式分解

1、我们以 4x² + 11x + 6 为例子，探究Slide and divide到底是如何工作的

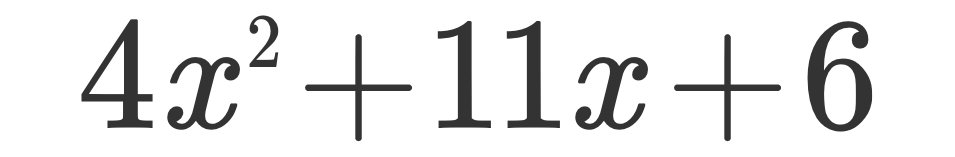
2、Slide

将二次项系数“滑”到常数项并相乘，也就是 4 × 6 = 24 

得到新的多项式 x² + 11x + 24

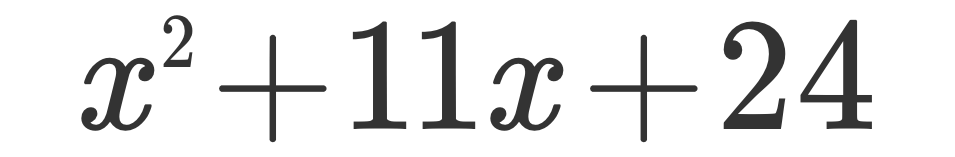
3、十字相乘分解

很容易就能看出 x² + 11x + 24 = (x + 3)(x + 8)

不能一眼看出的请多多加油，不知道十字相乘的同学请点击下面的链接

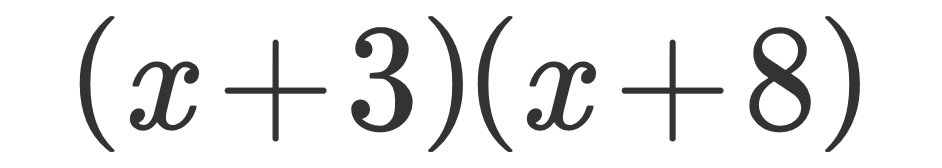
4、Divide

将所有的常数项除以原多项式 (4x² + 11x + 6) 的二次项 (4)

得到 (x + 3/4)(x + 8/4)

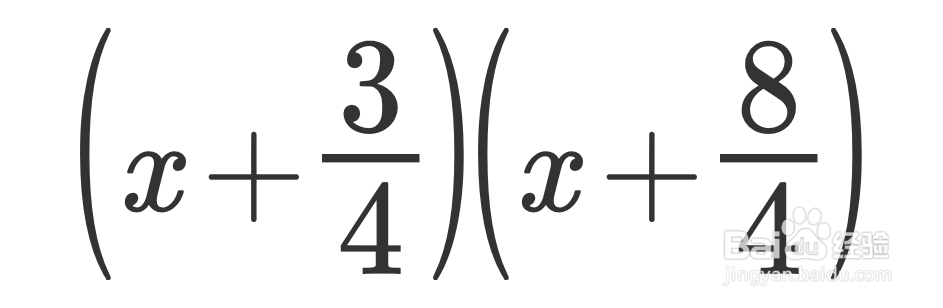
5、对一次项进行约分

得到 (x + 3/4)(x + 2/1)

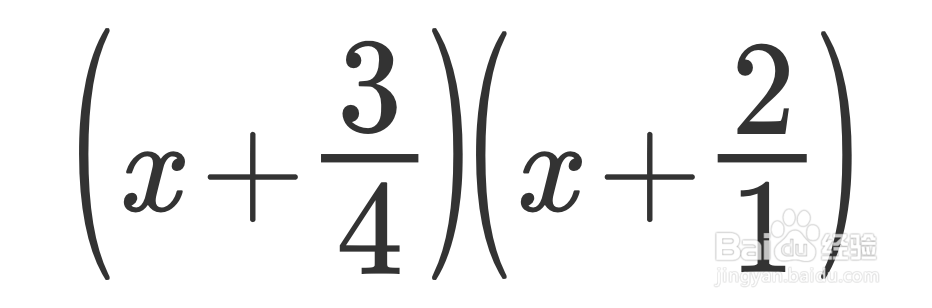
6、将分母Slide回各个括号的一次项

得到 (4x + 3)(x + 2)

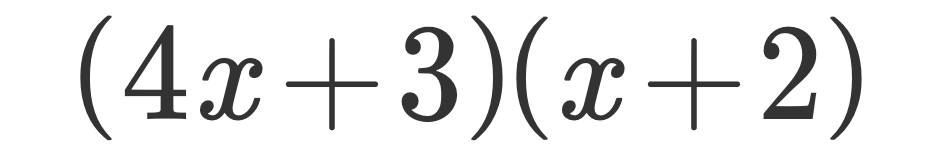
7、虽然上一步令人觉得不可思议，但是确实我们做到了！

1、那么我们看看怎么用 Slide and divide 分解 ax² + bx + c 

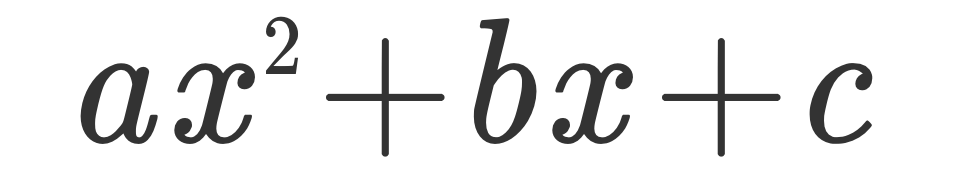
2、Slide

还是将二次项系数“滑”到常数项并相乘，也就是 ac

得到新的多项式 x² + bx + ac

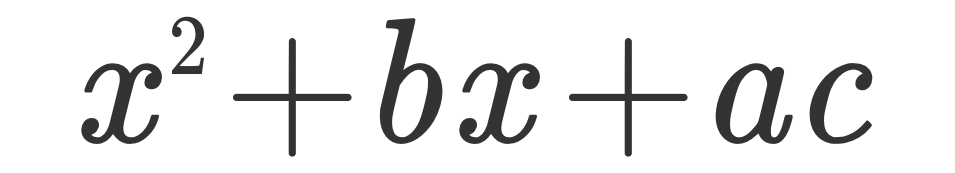
3、构造完全平方

x² + 2*(b/2)x + (b/2)² - (b/2)² + ac

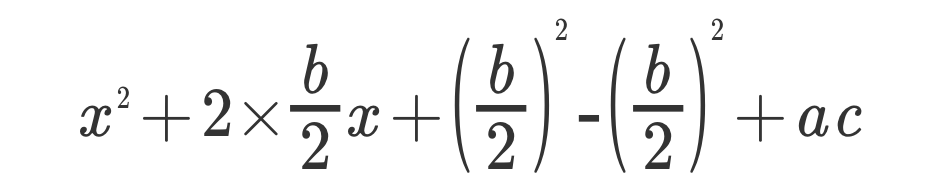
4、整理，准备使用平方差

(x + b/2)² - (b² - 4ac)/4

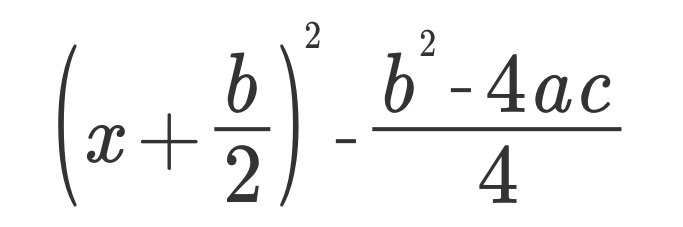
5、分解完成，准备Divide

(x + (b + √(b² - 4ac)) / 2)(x + (b - √(b² - 4ac)) / 2)

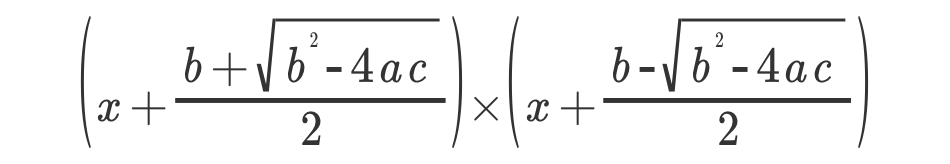
6、Divide

将所有的常数项除以原多项式 (ax² + bx + c) 的二次项 (a)

得到 (x + (b + √(b² - 4ac)) / 2a)(x + (b - √(b² - 4ac)) / 2a)

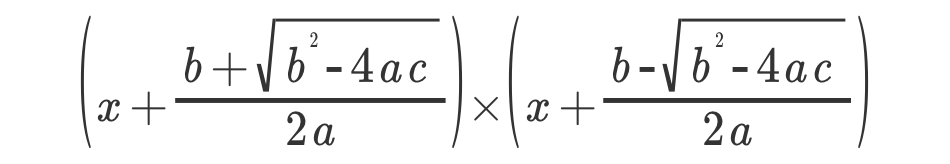
7、对一次项进行约分

假定 约分后为 n1/m1 和 n2/m2

得到 (x + n1/m1)(x + n2/m2)

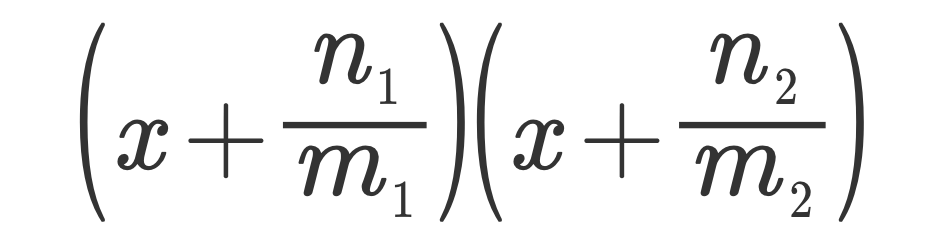
8、将分母Slide回各个括号的一次项

得到 (m1x + n1)(m2x + n2)

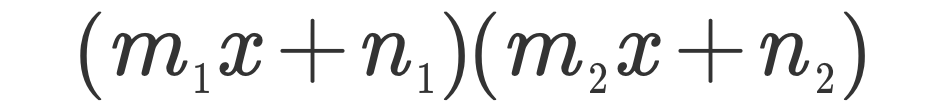
9、没错，这就是通用步骤，其中构造完全平方再用平方差的部分在实际情况中可以使用十字相乘。是不是开始觉得全是字母有点晕乎乎的了呢？

1、我们正常地操作 ax² + bx + c

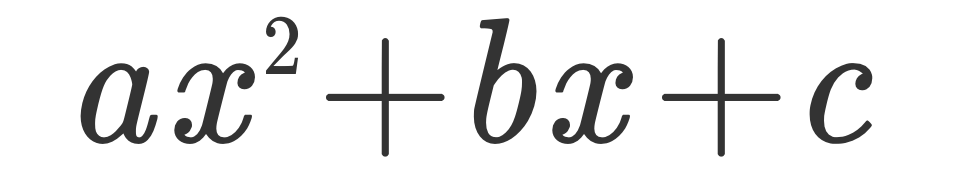
2、把 a 提出来

既方便构造，又和Slide and divide一样二次项系数为1

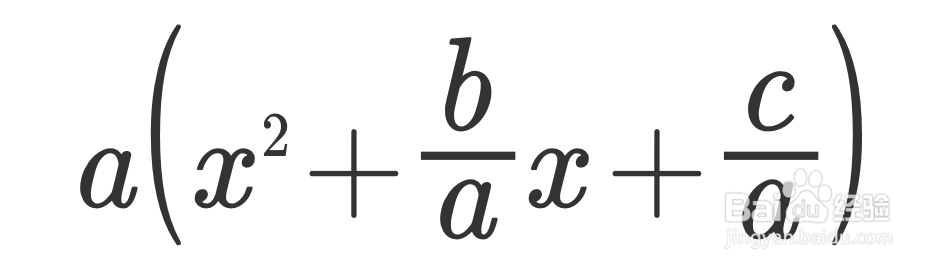
3、构造完全平方

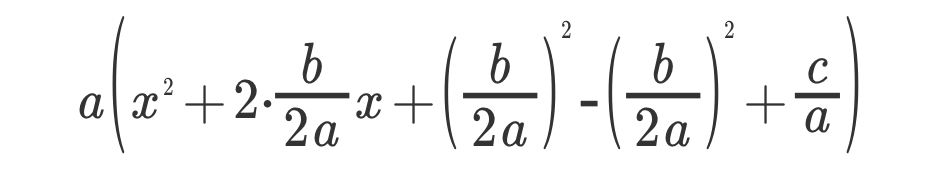
4、整理，准备使用平方差

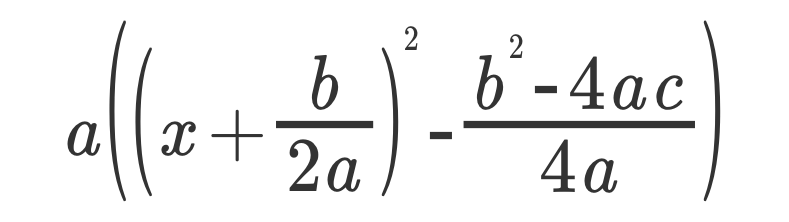
5、整理平方差过后的式子，只要约分，再把外面的 a 合理分配到括号中消掉大部分分母 （很明显，因为分母是 2a ）

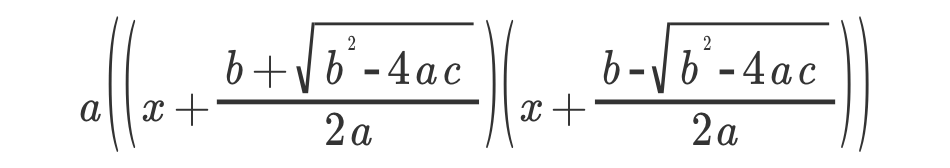
6、是不是看起来特别像呢（这是之前Slide and divide 约分前的样子）？

明白为什么 Slide and divide 是一种行之有效地方法了吗？

大概能想到为什么最后分母要Slide到一次项当系数了吗？