如何用几何证明算数平均数大于等于几何平均数

1、一、首先在图纸上画一个以b为边长的正方形，在沿着正方形的右边往下量，在距a的距离，画一条与正方形上边相平行的线。之后再画一条由左上到右下的线段，具体如下图所示。

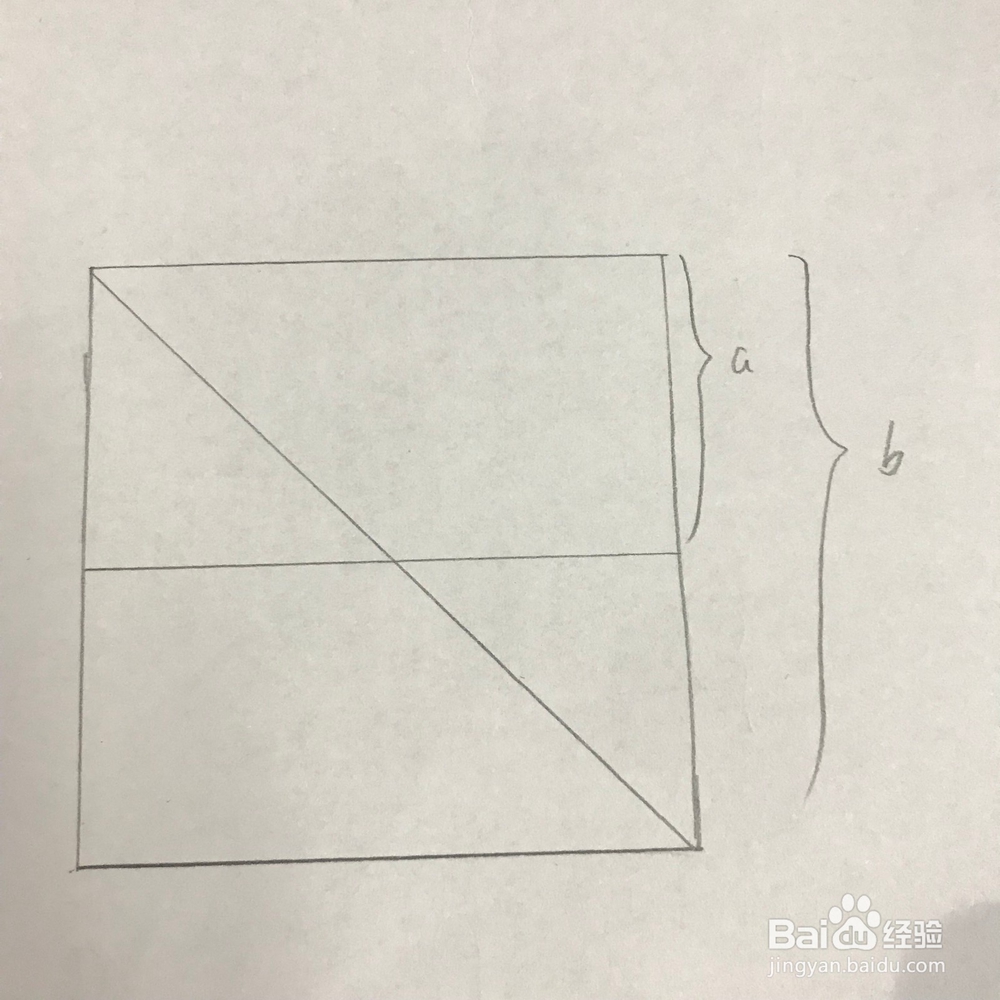
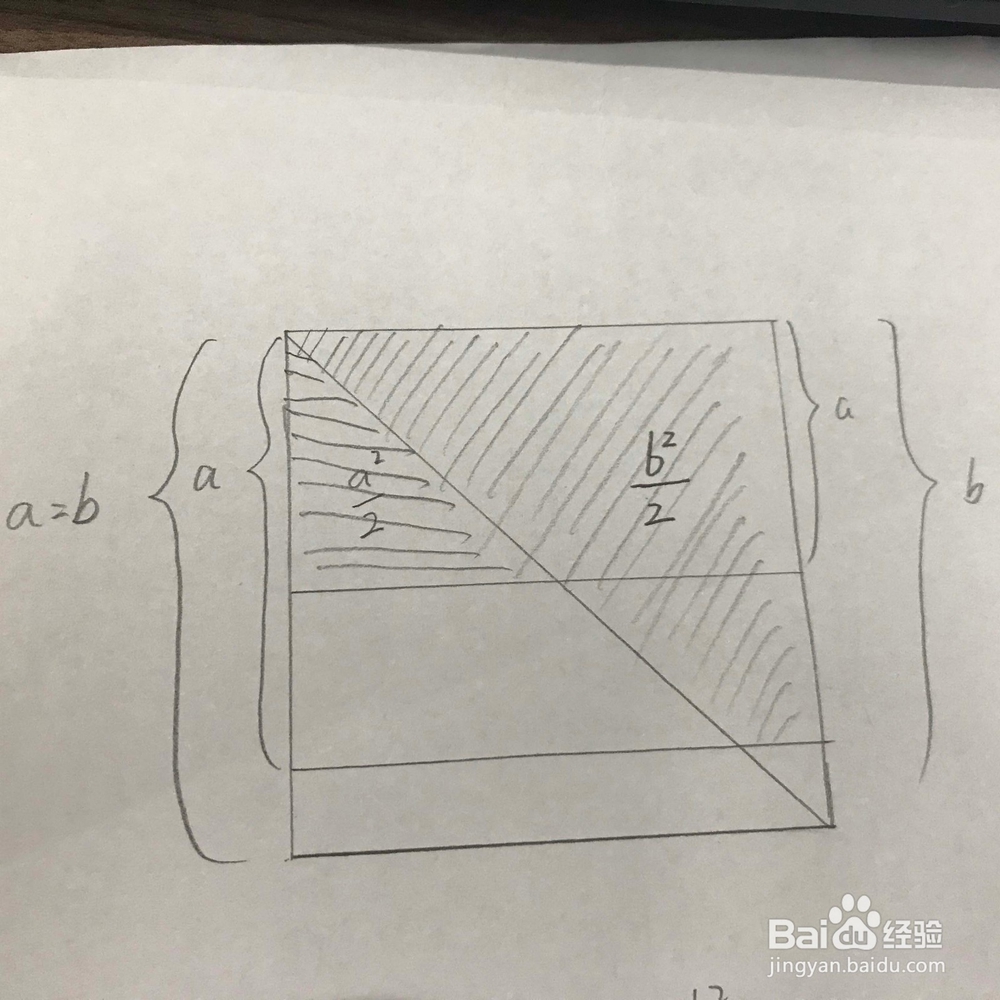
2、二、在画好的图形中，我们可以比较方面的计算得出正方形的面积，这里使用b的平方来表示。同时，我们也可以计算出由线段截出来的右上部分的三角形的面积，为二分之b的平方。

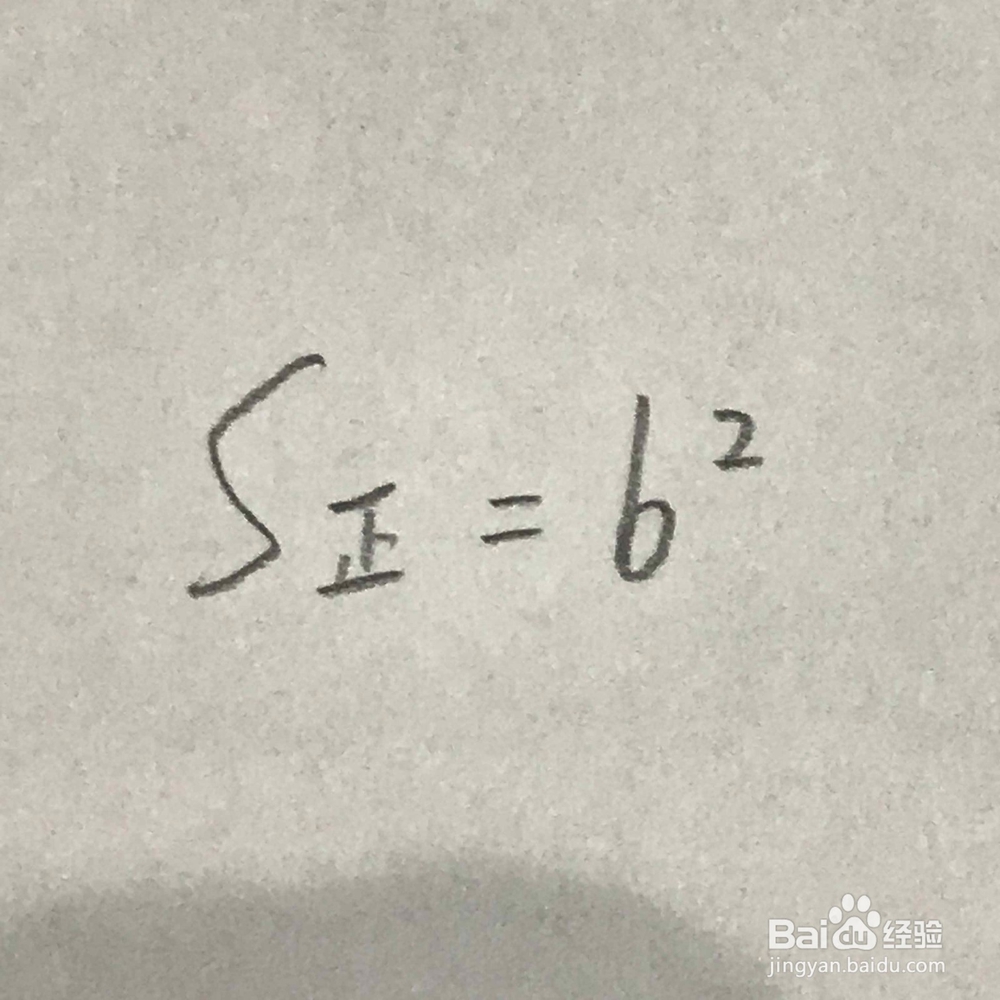
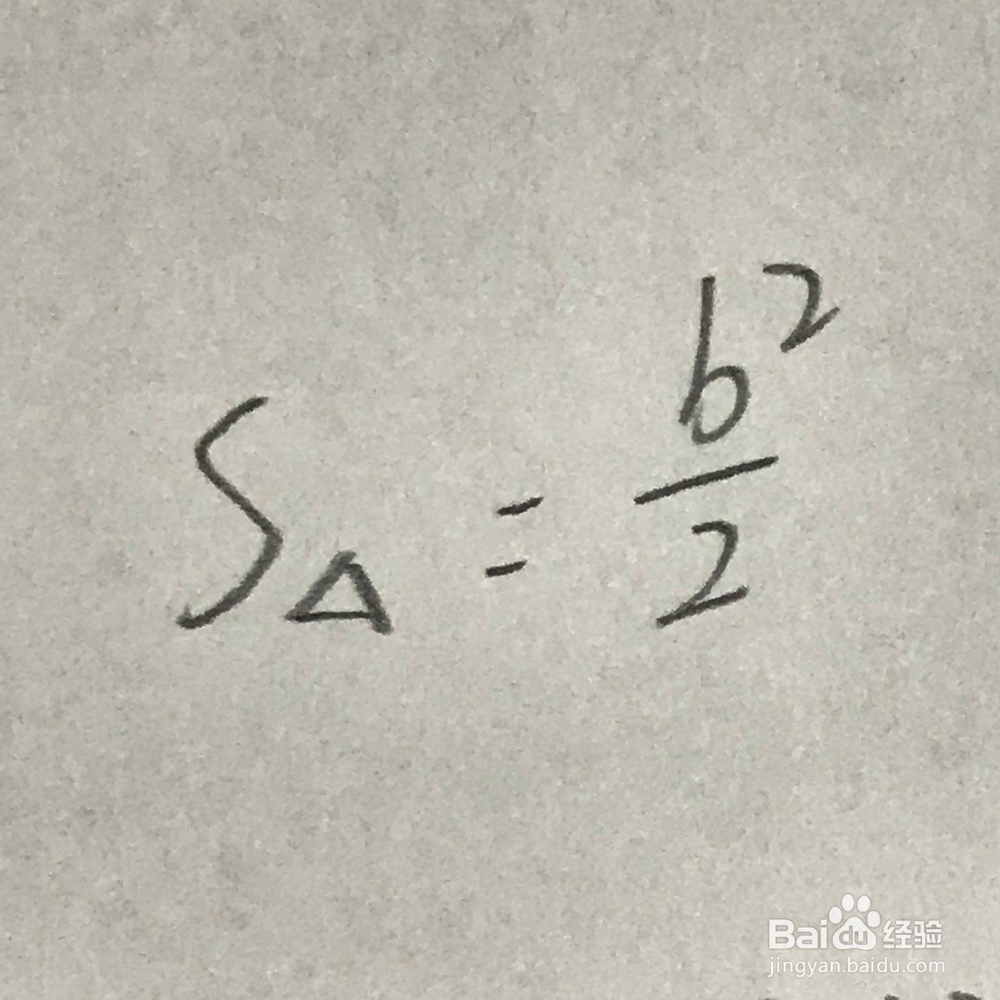
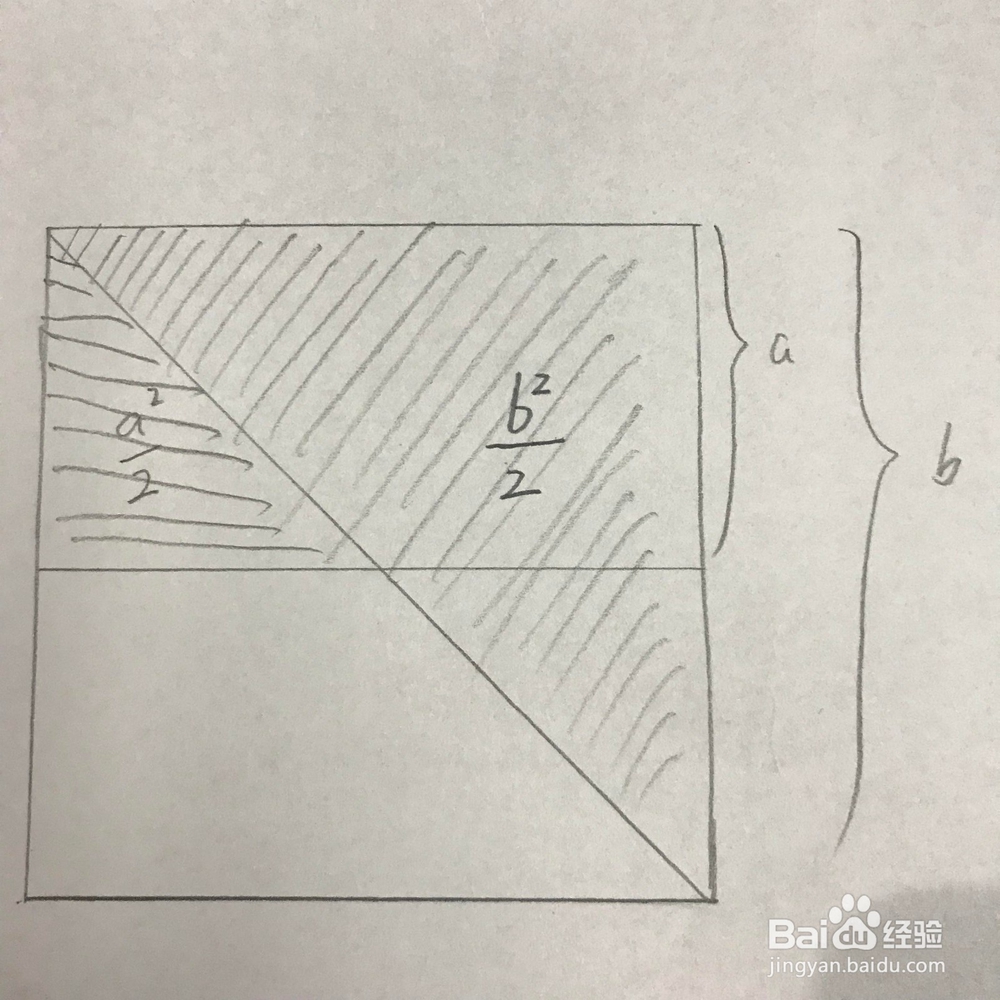
3、三、通过计算，我们知道，下图中的阴影部分的面积为二分之b的平方与二分之一a的平方之和。

4、四、并且可以很清楚的看到，阴影部分的面积是明显大于其中阴影部分的面积之和的。

5、五、当a的长度无限接近于b的长度的时候，或者a的长度与b的长度吻合的时候，这个时候则算数平均数与几何平均数相等了。

6、六、使用基本的可以理解的公式也同样可以证明，具体的证明算法如下图所示。