cos(lnx)的不定积分是什么

令t屏顿幂垂=√x, x=t^2 .dx=2tdt。∫√xsin√xdx=2∫t^2sintdt=-2∫t^2颊俄岿髭dcost。

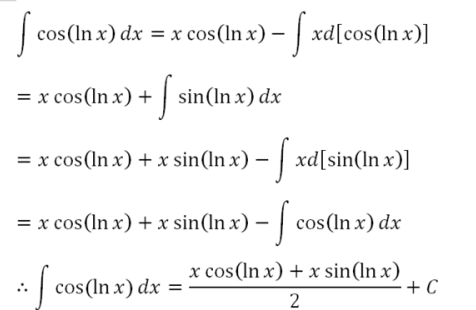
再分部积分=-2（t^2cost-∫2tcost dt）= -2t^2cost +4∫t d sint。

再分部积分=-2t^2 cost +4(t sint -∫ sint dt) =-2t^2 cost +4t sint +4 cost +C。

令lnx=t 则原式化为cos(t)e^t dt 这个用两次分部积分就出来了 详细过程如下： 积分cos(t)e^t dt=cos(t)e^t+积分sin(t)e^t dt=cos(t)e^t+sin(t)e^t-积分cos(t)e^t dt。

将上式中积分cos(t)e^t dt移项得：2*积分cos(t)e^t dt=cos(t)e^t+sin(t)e^t 所以答案就是【cos(t)e^t+sin(t)e^t】/2 换成x就是：【xcos(lnx)+xsin(lnx)】/2。