因式分解x²-3x+2
x²-3x+2因式分解为:x²-3x+2 =x×x+(-2-1)x+2×1 =(x-1)(x-2),运用了十字相乘法。
把一个多项式在一个范围(如实数范围内分解,即所有项均为实数)化为几个整式的积的形式,这种式子变形叫做这个多项式的因式分解,也叫作把这个多项式分解因式。

因式分解主要有十字相乘法,待定系数法,双十字相乘法、解方程法、配方法、分组分解法等。
1、提公因式法
如果一个多项式的各项有公因式,可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式,这种分解因式的方法叫做提公因式法。公因式可以是单项式,也可以是多项式。
例:
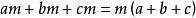
2、公式法
如果把乘法公式的等号两边互换位置,就可以得到用于分解因式的公式,用来把某些具有特殊形式的多项式分解因式,这种分解因式的方法叫做公式法。
分解公式:
(1)平方差公式:即两个数的平方差,等于这两个数的和与这两个数的差的积。
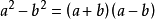
(2)完全平方公式:即两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和 (或差)的平方。
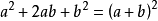
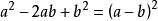
(3)立方和公式:即两数之和,乘它们的平方和与它们的积的差,等于这两个数的立方和。
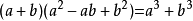
(4)立方差公式:即两数之差,乘它们的平方和与它们的积的和,等于这两个数的立方差。
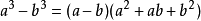
(5)完全立方公式:即两数之和(差)的立方等于这两个数的立方和(差)与每一个数的平方乘以另一个数3倍的和(和与差)。
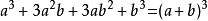
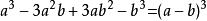
2、十字相乘法
对于
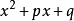
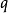
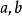
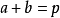
的系数),那么
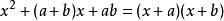
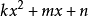
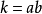
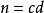
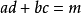
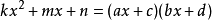
相乘法。
具体方法:十字左边相乘等于二次项系数,右边相乘等于常数项,交叉相乘再相加等于一次项。
3、双十字相乘法
对于某些二元二次六项式
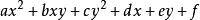
4、解方程法
通过解方程来进行因式分解的方法叫做解方程法。
例:把x2-6x+8=0 分解因式
解:原方程解得x1=2,x2=4,就得到原式=(x-2)(x-4)
5、配方法
对于某些不能利用公式法的多项式,可以将其配成一个完全平方式,然后再利用平方差公式,就能将其因式分解,这种分解因式的方法叫做配方法。属于拆项、补项法的一种特殊情况。也要注意必须在与原多项式相等的原则下进行变形。
例:分解因式x2+3x-40
解:x2+3x-40
=x2+3x+2.25-42.25
=(x+1.5)2-(6.5)2
=(x+8)(x-5).
6、分组分解法
通过分组分解的方式来分解提公因式法和公式分解法无法直接分解的因式,这种分解因式的方法叫做分组分解法。能分组分解的多项式有四项或大于四项,一般的分组分解有两种形式:二二分法,三一分法。
扩展资料
因式分解步骤:
1、如果多项式的首项为负,应先提取负号;
这里的“负”,指“负号”。如果多项式的第一项是负的,一般要提出负号,使括号内第一项系数是正的。
2、如果多项式的各项含有公因式,那么先提取这个公因式,再进一步分解因式;
要注意:多项式的某个整项是公因式时,先提出这个公因式后,括号内切勿漏掉1;提公因式要一次性提干净,并使每一个括号内的多项式都不能再分解。
3、如果各项没有公因式,那么可尝试运用公式、十字相乘法来分解;
4、如果用上述方法不能分解,再尝试用分组、拆项、补项法来分解。
口诀:先提首项负号,再看有无公因式,后看能否套公式,十字相乘试一试,分组分解要合适。
参考资料:百度百科-因式分解